7. Multiplicative Functionals#
Authors: Jaroslav Borovicka, Lars Peter Hansen, and Thomas Sargent
Date: November 2025
\(\newcommand{\eqdef}{\stackrel{\text{def}}{=}}\)

Challenges in navigating long-term uncertainty.
Chapter 4:Processes with Markovian increments described additive functionals of a Markov process. This chapter describes exponentials of additive functionals that we call multiplicative functionals. We can use them to model stochastic growth, stochastic discounting, belief distortions and their interactions. After adjusting for geometric growth or decay, a multiplicative functional contains a martingale component that turns out to be a likelihood ratio process that is itself a special type of multiplicative functional called an exponential martingale. By simply multiplying random variables of interest by the multiplicative martingale prior to computing conditional expectations under a baseline probability, we construct an alternative probability measure. It functions as a relative density that alters the baseline probability measure. For an initial application of multiplicative functionals to asset valuation and investor preferences, see [Anderson et al., 2003]. We will explore these and other applications in discussions that follow. We will see that multiplicative functionals has several applications. They allow us to characterize components of stochastic growth and stochastic discounting that persist over long time horizons. They show how macroeconomic shocks with long-term impacts are reflected in asset pricing. They provide a tractable modeling tool for models in which investors have subjective beliefs that may deviate from a baseline probability and allow for measuring their magnitudes using statistical discrimination measures. We will encounter several other applications of multiplicative functionals, including models of returns and positive cash flows that compound over multiple horizons, cumulative stochastic discount factors are used to long-horizon, risk-return tradeoffs.
7.1. Geometric growth and decay#
To construct a multiplicative functional, we start with an underlying Markov process \(X\) that has a stationary distribution \(Q\), and we suppose that \(Y_0\) and \(X_0\) depend only on date zero information summarized by \({\mathfrak A}_0.\)
Definition 7.1
Let \(Y \eqdef \{ Y_t\}\) be an additive functional that as in Chapter 4 is described by
where \(X_t\) is the time \(t\) component of a Markov state vector satisfying \(X_{t+1} = \phi(X_t, W_{t+1})\) and \(W_{t+1}\) is the time \(t+1\) value of a martingale difference process (\({\mathbb E} \left(W_{t+1} \mid {\mathfrak A}_t \right) = 0 \)) of unanticipated shocks. We say that \(M \eqdef \{M_t: t \ge 0 \} = \{ \exp(Y_t) : t \ge 0 \}\) is a multiplicative functional parameterized by \(\kappa\).
An additive functional grows or decays linearly, so the exponential of an additive functional grows or decays geometrically. We construct a multiplicative functional recursively by
We may solve for \(N_{t+1},\)
When \(M_t\) is zero, so is \(M_{t+1}.\) In this case, the random variable, \(N_{t+1},\) is not uniquely defined by (7.1). Our decision to set it to unity is simply a convenient normalization. In light of (7.1), we refer to \(N\) as the multiplicative increment of the process \(M\).
Chapter 4 stated a Law of Large Numbers and a Central Limit Theorem for additive functionals. In this chapter, we use other mathematical tools to analyze the limiting behavior of multiplicative functionals.
7.2. Special multiplicative functionals#
We define the three primitive multiplicative functionals.
Example 7.1
Suppose that \(\kappa = \eta\) is constant and that \(M_0\) is a Borel measurable function of \(X_0\). Then
This process grows or decays geometrically.
Example 7.2
Suppose that
Then
so that
A multiplicative functional that satisfies (7.2) is called a multiplicative martingale. We denote such a process as \(M \eqdef L\) because it is appropriate to view it as likelihood ratio process. We will have more to say about this in some of the discussion that follows. It will often be convenient to initialize this process at \(M_0 = L_0 = 1.\)
Example 7.3
Suppose that \(M_t = \exp\left[h(X_t)\right]\) where \(h\) is a Borel measurable function. The associated additive functional satisfies
and is parameterized by \(\kappa(X_t, W_{t+1}) = h\left[ \phi(X_t, W_{t+1} ) \right] - h(X_t)\) with initial condition \(Y_0 = h(X_0)\).
When the process \(\{X_t\}\) is stationary and ergodic, multiplicative functional Example 7.1 displays expected growth or decay, while multiplicative functionals Example 7.2 and Example 7.3 do not. Multiplicative functional Example 7.3 is stationary, while Example 7.1 and Example 7.2 are not.
We can construct other multiplicative functionals simply by multiplying instances of these primitive ones. Soon we shall reverse that process by taking an arbitrary multiplicative functional and (multiplicatively) decomposing it into instances of our three types of multiplicative functionals. Before doing so, we explore multiplicative martingales in more depth.
7.3. Multiplicative martingales#
We can use multiplicative martingales to represent alternative probability models. We can characterize an alternative model with a set of implied conditional expectations of all bounded random variables, \(B_{t+1},\) that are measurable with respect to \({\mathfrak A}_{t+1}\). The constructed conditional expectation is
We want multiplication of \(B_{t+1}\) by \(N_{t+1}\) to change the baseline probability to an alternative probability model. To accomplish this, the random variable \(N_{t+1}\) must satisfy:
\(N_{t+1} \ge 0\);
\({\mathbb E}\left(N_{t+1} \mid {\mathfrak A}_t \right) = 1\);
\(N_{t+1}\) is \({\mathfrak A}_{t+1}\) measurable.
Property 1 is satisfied because conditional expectations map positive random variables \(B_{t+1}\) into positive random variables that are \({\mathfrak A}_t\) measurable. Properties 2 and 3 are satisfied because \(N\) is the multiplicative increment of a multiplicative martingale. The resulting process \(L\) can be viewed as a likelihood ratio or Radon-Nikodym derivative process for the alternative probability measure relative to the baseline measure.
Representing an alternative probability model in this way is restrictive. For instance, if a nonnegative random variable has conditional expectation zero under the baseline probability, it will also have zero conditional expectation under the alternative probability measure, an indication of absolute continuity of the implied probability measure with respect to the baseline measure. Two models that violate absolute continuity can be distinguished with probability one from only finite samples. To avoid this degenerate outcome, likelihood-based statistically inference typically imposes this form of absolute continuity.
Given the multiplicative construction, the implied alternative conditional probability measure over \(\tau\) periods uses the random variable
to compute the \(\tau\) time-period-ahead conditional expectation. With this construction, the \(\tau\)-period conditional expectation may be computed by iterating on the one-period conditional expectations in accordance with the Law of Iterated expectations.
Multiplicative martingales provide a way to model diverse subjective beliefs of private agents or policy-makers within dynamic, stochastic equilibrium models when these beliefs are allowed to depart from the model builder’s model. As [Hansen and Scheinkman, 2009] show, they also offer a way to value cumulative returns. Let \(R_t\) be a multiplicative process that measures a cumulative return between date \(t\) and date zero. Let \(S_t\) be a corresponding equilibrium discount factor between these same two dates. That \(L = RS\) is a multiplicative martingale follows from equilibrium restrictions on one-period returns. That is,
where \(S_{t+1}/{S_t}\) is the one-period stochastic discount factor and \(R_{t+1}/{R_t}\) is the one-period gross return. For the application, we construct
Here are some examples of multiplicative martingales constructed from some standard probability models.
Example 7.4
Consider a baseline Markov process having transition probability density \(\pi_o\) with respect to a measure \(\lambda\) over the state space \(\mathcal{X}\)
Let \(\pi\) denote some other transition density that we represent as
where we assume that \(\pi_o(x^+ \mid x) = 0\) implies that \(\pi(x^+ \mid x) = 0\) for all \(x^+\) and \(x\) in \(\mathcal{X}\).
Construct the multiplicative increment process as:
Example 7.5
Let an alternative model for a vector \(X\) be a vector autoregression:
where \({\mathbb A}\) is a stable matrix, \(\{W_{t+1} : t \ge 0 \}\) is an i.i.d. sequence of \({\cal N}(0,I)\) random vectors conditioned on \(X_0,\) and \({\mathbb B}\) is a square, nonsingular matrix. Assume that a baseline model for \(X\) has the same functional form but different settings \(({\mathbb A}_o, {\mathbb B}_o)\) of its parameters. Construct \(N_{t+1}\) as the one-period conditional log-likelihood ratio
Notice how the matrices \(({\mathbb A}_o, {\mathbb B}_o)\) of the baseline model and parameters \(({\mathbb A}, {\mathbb B})\) of the alternative model both appear.
Remark 7.1
Because \(\mathbb{B}\) is a nonsingular square matrix, model Example 7.5 has the same number of shocks, i.e., entries of \(W\), as there are components of \(X\). A more general setting would be a hidden Markov state model like one presented in Section Kalman Filter and Smoother of Chapter Hidden Markov Models that has a time-invariant representation with an ``information state vector’’ constructed as a way to condition on an infinite past of an observation vector.
We can elicit a limiting behavior of multiplicative martingales by applying Jensen’s inequality to the concave function \(\log L\) depicted in Fig. 7.1 based on
where we normalize \(L_0 = 1\).
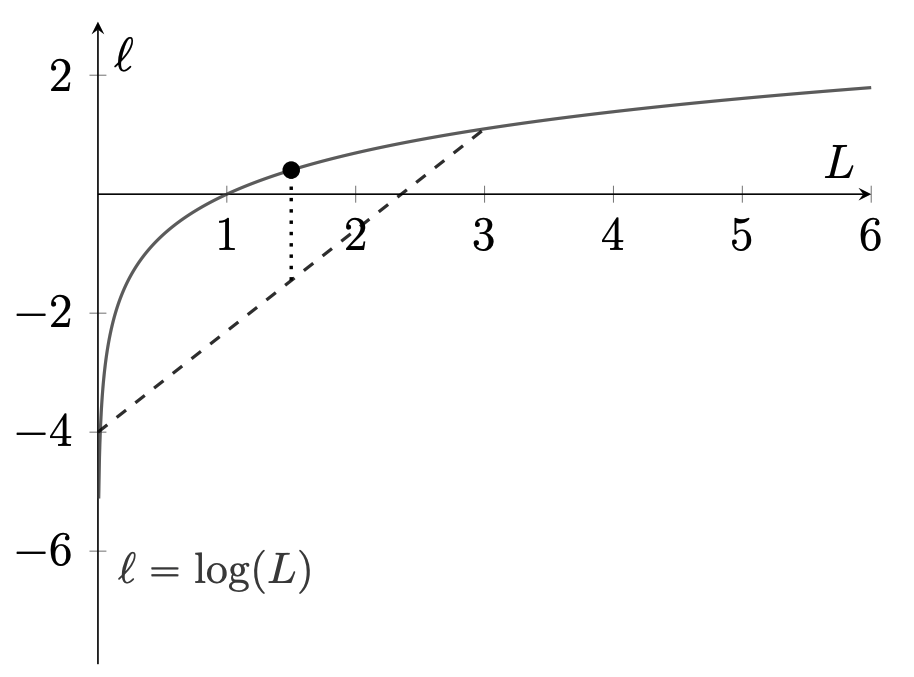
Fig. 7.1 Jensen’s Inequality. The logarithmic function is a concave function that equals zero when evaluated at unity. The line segment lies below the logarithmic function.An interior average of endpoints of the straight line lies below the logarithmic function.#
Moreover, by Jensen’s inequality,
for \(N_{t+1}\) satisfying \(L_{t+1}= N_{t+1} L_t.\). Note that
This implies that under the baseline model the log-likelihood ratio process \(L\) is a supermartingale relative to the information sequence \(\{ {\mathfrak A}_t : t\ge 0\}\).
From the Law of Large Numbers as described Chapter 1:Laws of Large Numbers and Stochastic Processes , a population mean is well approximated by a sample average from a long time series. That opens the door to discriminating between two models. Under the baseline model, the log likelihood ratio process scaled by \(1/t\) converges to a negative number. If the baseline model, actually generates the data, the expected log likelihood ratio constructed with data will (at least eventually) be negative except in the degenerate case in which \(N_{t+1} = 1\) with probability one. Such a calculation justifies discriminating between the two models by calculating \(\log L_{t}\) and checking if it is positive or negative. This procedure amounts to an application of the method of maximum likelihood. Sometimes
is used as a measure of statistical divergence.
Suppose now that we reverse the roles of the baseline and alternative probability measures.
Definition 7.2
The conditional relative entropy of a martingale increment is defined to be:
This entity is sometimes referred as Kullback-Leibler divergence. To understand why conditional relative entropy is nonnegative, observe that multiplication of \(\log N_{t+1}\) by \(N_{t+1}\) changes the conditional probability distribution for which the conditional expectation of \(\log N_{t+1}\) is calculated from the baseline model to the alternative model. The function \( n \log n\) is convex and equal to zero for \(n=1\). Therefore, Jensen’s inequality implies that conditional relative entropy is nonnegative and equal to zero when \(N_{t+1} = 1\)
conditioned on \({\mathfrak A}_t\).
Notice that
Thus \(L \log L\) is a submartingale. The expression
and is a measure of relative entropy over a \(t\)-period horizon. Relative entropy is often used to analyze model misspecifications and also appears in statistical characterizations of “large deviations” for Markov processes and in information theory.
Remark 7.2
Consider a simple version of likelihood-based model identification. Suppose that a decision-maker does not know whether a baseline or alternative model generates the data. Attach a subjective prior probability \(\pi_o\) to the baseline probability model and probability \(1 - \pi_o\) on the alternative. Let \(L\) be a likelihood ratio process with \(L_t\) reflecting information available at date \(t\). Date \(t\) posterior probabilities for the baseline and alternative probability models are:
When \({\frac 1 {t}} \log L_{t}\) converges to a negative number under the baseline probability, the first probability converges to one. But when \({\frac 1 {t}} \log L_{t}\) converges to a positive number under the alternative probability, the second probability converges to one. When the data are generated by the baseline probability model, the Law of Large Numbers implies the former; and when the data are generated by the alternative probability model, the Law of Large Numbers implies the latter. This shows that model selection based on posterior probabilities will eventually determine which model generated the data, the baseline model or the alternative model. This analysis can be extended to situations in which some other model generates the data.
Remark 7.3
Martingales that represent changes of measure appear in asset pricing models that posit a difference between a representative investor’s ‘’subjective’’ model and a distinct model that a researcher assumes actually governs the data. Author of such asset pricing models distinguish them from rational expectations models that adhere to a ‘’communism of beliefs’’ whereby the representative agent, nature, and perhaps an economic model builder share the same probability model. Parts of the behavioral finance literature appeal to insights from psychology to motivate violations of that ``communism of beliefs’’ axiom. The tools here can help us interpret such models by leading us to think about sources of those model discrepancies in terms of the understandings and motivations that might lead a sophisticated investor to acknowledge possible discrepancies between a subjective model and the type of baseline approximating model commonly used in asset pricing models. Using martingales to represent belief distortions allows us to sharpen some substantial issues addressed in the in the behavioral finance literature. For example, in that literature we often read about over and under reaction, but over and under reaction, but those reactions must be relative to some other measure. Our framework invites us to drill down on the source of the martingale that accounts those reactions? For example, statistical discrepancy measures might tell us that it is very difficult for sophisticated statisticians to distinguish or select among alternative approximating models to describe the data. Presumably, some such belief distortions on the part of investors are likely to persist when such statistical challenges for the investors and econometricians are substantial.
Remark 7.4
These tools are also pertinent to the study of models in which investors have heterogeneous beliefs. [Alchian, 1950] and [Friedman, 1953], among others, have argued that investors with distorted beliefs will eventually be driven out of the market by investors with more accurate perceptions of the future because of the relative success of the latter type of investors. This has been one argument for imposing rational expectations in asset pricing models. [Kogan et al., 2006] refine this view by breaking a simple link between survival and price impact of the investors with distorted beliefs. [Borovička, 2020] goes further by characterizing families of investor preferences for which the investors with the distorted beliefs survive in the long run. These latter two contributions feature differences in how investors look at stochastic growth. A continuous-time counterpart to the martingale representation for belief distortions that we describe and characterize in this chapter are featured in both the [Kogan et al., 2006] and the [Borovička, 2020] papers.
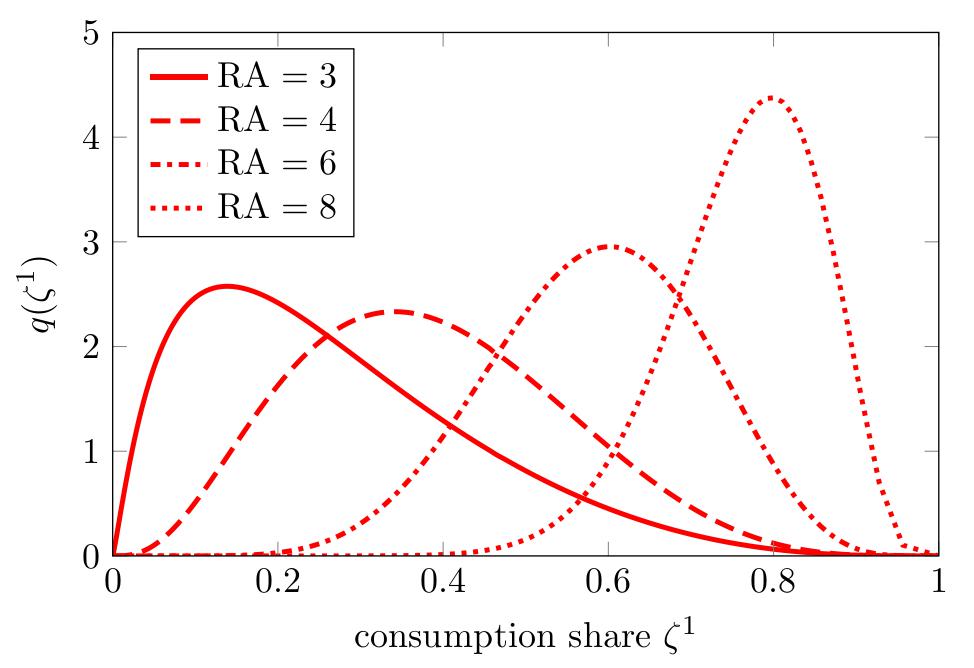
This figure is from [Borovička, 2020]. It plots the stationary densities for the fraction of aggregate consumption allocated to the first of two types of investors. The first is mistakenly optimistic about future consumption growth. The second knows the correct evolution. The figure illustrates that both consumers “survive” in the long run and that the allocation shifts in favor of the optimistic investor when both are more risk averse.
7.4. Factoring a multiplicative functional#
Following [Hansen and Scheinkman, 2009] and [Hansen, 2012], we factor a multiplicative functional into three multiplicative components having the primitive types Example 7.1, Example 7.2, Example 7.3.
As in definition Definition 7.1, let \(Y\) be an additive functional, and let \(M = \exp(Y)\). Apply a one-period operator \(\mathbb{M}\) defined by
to bounded Borel measurable functions \(f\) of the Markov state. By applying the Law of Iterated expectations, a two-period operator iterates \(\mathbb{M}\) twice to obtain:
with corresponding definitions of \(j\)-period operators \(\mathbb{M}^j\). The family of operators is a special case of what is called a ``semi-group.’’ The domain of the semigroup can typically be extended to a larger family of functions, but this extension depends on further properties of the multiplicative process used to construct it.
We next derive a revealing representation of this semigroup by factoring the multiplicative functional \(M\) in an interesting way. We achieve this by applying what is referred to in mathematics as Perron-Frobenius theory based on the following equation:
Eigenvalue-eigenfunction Problem: Solve
for an eigenvalue \(\exp(\tilde \eta)\) and a positive eigenfunction \({\tilde e}\).
Consistent with Perron-Frobenius theory, call the positive eigenvalue, the principal eigenvalue, and the associated positive eigenvector, the principal eigenfunction, of the operator \(\mathbb{M}\).
Use the principal eigenvalue and eigenvector, and define:
Note that we constructed \({\widetilde N}_{t+1}\) so as to have a conditional expectation equal to unity. Using \({\widetilde N}\) as a martingale increment process, build
Theorem 7.1
Let \(M\) be a multiplicative functional. Suppose that the principal eigenvalue-eigenfunction problem has a solution with principal eigenfunction \({\tilde e}(X)\). Then the multiplicative functional is the product of three components that are instances of the primitive functionals in examples Example 7.1, Example 7.2, and Example 7.3:
where \({\widetilde L}_t\) is a multiplicative martingale.
The factorization of a multiplicative functional described in Theorem 7.1 is a counterpart to the Chapter 4 Proposition 4.1 decomposition of an additive functional. We used the Proposition 4.1 martingale to identify the permanent component of an additive functional in Chapter 4. In this chapter, we shall use the multiplicative martingale isolated by Theorem 7.1 to represent a change of probability measure, but one that will help us understand long-term risk return tradeoffs.
Models in which \(X\) is a finite-state Markov chain are givea direct computation in which the principal eigenvalue calculation reduces to finding an eigenvector of a matrix with all positive entries.
Example 7.6
The stochastic process \(X\) is governed by a finite-state Markov chain on state space \( \{ {\sf s}_1, {\sf s}_2, \ldots, {\sf s}_n \}\), where \(s_i\) is the \(n \times 1\) vector whose components are all zero except for \(1\) in the \(i^{th}\) row. The transition matrix is \({\mathbb P},\) where \({\sf p}_{ij} = \textrm{Prob}( X_{t+1} = {\sf s}_j | X_t = {\sf s}_i)\). We represent the Markov chain as
where \({\mathbb E} (X_{t+1} | X_t ) = {\mathbb P}' X_t \), \({\mathbb P}'\) denotes the transpose of \({\mathbb P}\), and \(W_{t+1}\) is an \(n \times 1\) vector process that satisfies \({\mathbb E} ( W_{t+1} | X_t) = 0 \), which is therefore a martingale-difference sequence adapted to \(X_t, X_{t-1}, \ldots , X_0\). Think of \(W_{t+1}\) as the vector of errors when forecasting \(X_{t+1}\) based on current information.
Let \({\mathbb G}\) be an \(n \times n\) matrix whose \((i,j)\) entry \({\sf g}_{ij}\) is an additive contribution to the growth that \(Y_{t+1} - Y_t\) experiences when \(X_{t+1} = {\sf s}_j\) and \(X_t = {\sf s}_i\). The stochastic process \(Y\) is governed by the additive functional
Let \(M= \exp(Y)\). Define a matrix \({\mathbb M}\) whose \((i,j)^{th}\) element is \({\sf m}_{ij} = \exp({\sf g}_{ij}).\) Represent the stochastic process \(M\) as the multiplicative functional:
Associated with this multiplicative functional is the principal eigenvalue problem
To convert this to a linear algebra problem, write the \(j^{th}\) entry of \({\tilde e}\) as \({\tilde e}_j\). Since \(X_t\) always assumes the value of one of the coordinate vectors \({\sf s}_i, i =1, \ldots, n\),
when \(X_t = {\sf s}_i\) and \(X_{t+1} = {\sf s}_j\). This allows us to rewrite the principal eigenvalue problem as
or
where \(\widetilde {\sf m}_{ij} \eqdef {\sf p}_{ij} {\sf m}_{ij}\) and \({\tilde e}_i\) is entry \(i\) of \({\tilde e}\).
Notice that this construction incorporates the transition probabilities into the construction of the matrix \({\widetilde {\mathbb M}}\). We do this to reduce the problem to one of finding an eigenvalue and corresponding eigenvector of a matrix. Specifically, we want the positive eigenvalue associated with a positive eigenvector of (7.9).
After solving the principal eigenvalue problem, we construct an alternative transition matrix for a finite-state Markov process. Construct
and form the matrix \({\widehat {\mathbb N}} = [{\widehat {\sf n}}_{ij}]\). The matrix \({\widehat {\mathbb N}}\) has entries that are nonnegative, and
which verifies that \({\widehat {\mathbb N}}\) can be viewed as a transition matrix.
Finally, we show how to construct the factorization of the \(M\) process. To build the martingale of interest, we must undo the probability scaling that we did when forming \({\widehat {\mathbb N}}.\) With this in mind, solve for \({\tilde n}_{ij}\) that satisfies:
where we arbitrarily set \({\tilde n}_{ij}\) equal one when \(p_{ij} = 0\) and build the matrix \({\widetilde {\mathbb N}} = [ {\widetilde n}_{ij}]\). These constructions allow us to write (7.8) as
Remark 7.5
Using the previous example, note that the matrix \(\widetilde {\mathbb M}\) could be inferred from the so-called Arrow prices. Specifically, given prices of all of the state contingent claims for next period, we can infer the column of \(\widetilde {\mathbb M}\) associated with the current state. By observing prices for all of the current states, all of the columns of \(\widetilde {\mathbb M}\). We only need to know \(\widetilde {\mathbb M}\) to pose and solve the principal eigenvalue problem and hence to construct transition probabilities as given by (7.10), but not the \({\sf p}_{ij}\)’s and the \({\sf s}_{ij}\)’s. This gives us a way to. recover a transition probabilities from asset prices in the language of [Ross, 2015]. Notice, in particular, that the \({\sf p}_{ij}\)’s and \({\sf s}_{ij}\)’s cannot be inferred uniquely from the \({\sf m}_{ij}\)’s. In particular, the Arrow prices are insufficient to identify the transition probabilities. Ross imposed restrictions on \({\sf s}_{ij}\)’s that implied that the recovered probabilities are actually the \({\sf p}_{ij}\)’s. In general, the recovered probabilities will differ from the baseline transition probability matrix. We will have more to say about this difference and investigate why the recovered probabilities remain interesting. See [Borovička et al., 2016] for an extended discussion of this claim.
The following log-linear, log-normal specification displays relevant mechanics of the multiplicative factorization with direct connection to the corresponding additive decomposition
Example 7.7
Consider a stationary \(X\) process and an additive \(Y\) process described by the VAR
where \({\mathbb A}\) is a stable matrix and \(\{ W_{t+1} : t \ge 0 \}\) is a sequence of independent and identically normally distributed random vectors with mean zero and covariance matrix \({\mathbb I}\). In Proposition 4.1 of Chapter 4, we described the decomposition
where
Let \(M_t = \exp(Y_t)\). Use equation (7.12) to deduce
where
and
While the additive martingale of \(Y= \log(M)\) has a variance that grows linearly over time, this variance contributes a component to the exponential trend of the multiplicative functional \(M\) along with an adjustment to the martingale component.
Example 7.8
Consider the following stochastic volatility example. Suppose that a scalar state variable evolve as first-order autoregression:
where \(\{W_{t+1} : t \ge 0 \}\) is an iid sequence of normally distributed random variables. The state variable \(X_t\) gives the source of volatility fluctuations. Guess a principle eigenfunction of the form:
and construct
Write the principle eigenfunction equation as:
where we took logarithms of both sides of the equation. The computation on left side of this equation has a tractable formula for expressing the outcome as a quadratic function of the state.
Solve the equation in three steps. First, equate coefficients on \(x^2\) and deduce a quadratic equation for \(\epsilon_2.\) Next, equate coefficients on \(x\) and obtain a linear equation for \(\epsilon_1\). Finally, equate constants obtain an equation for \({\tilde \eta}\). The initial quadratic equation is
When it has a solution, there is will typically be two possible choices. For the solution to be of interest, \(1 - \epsilon_2 {\sf b}^2\) must be positive.
Second, equate coefficient on \(x\) to solve an equation for \(\epsilon_1\) given \(\epsilon_2\):
Third, we solve for \({\tilde \eta}\) by equating the constant and plugging the solutions for \(\epsilon_1\) and \(\epsilon_2\):
For this example,
where \(\propto\) means proportional to up to a scale factor that depends on \(X_t\). Under the implied change in measure, \(W_{t+1}\) is distributed as normal random variable with conditional mean
and precision \(1 - \epsilon_2 {\sf b}^2\). Under the change of probability measure, \(W_{t+1}\) remains normally distributed with a different variance and state-dependent mean. Under this change in probability measure, the \(X\) remains a first-order autoregression but with different dynamics. It could, for instance, be an explosive autoregression.
Remark 7.6
The martingale component of the multiplicative functional has “peculiar behavior.” It has expectation one by construction. The Martingale Convergence Theorem guarantees that sample paths converge, typically to zero. The Martingale Convergence Theorem is operative because the positive martingale is bounded from below. Since its date zero conditional expectation is one, for long horizons this process necessary has a fat right tail. Fig. 7.2 plots probability density functions of the martingale component for different values of \(t\).
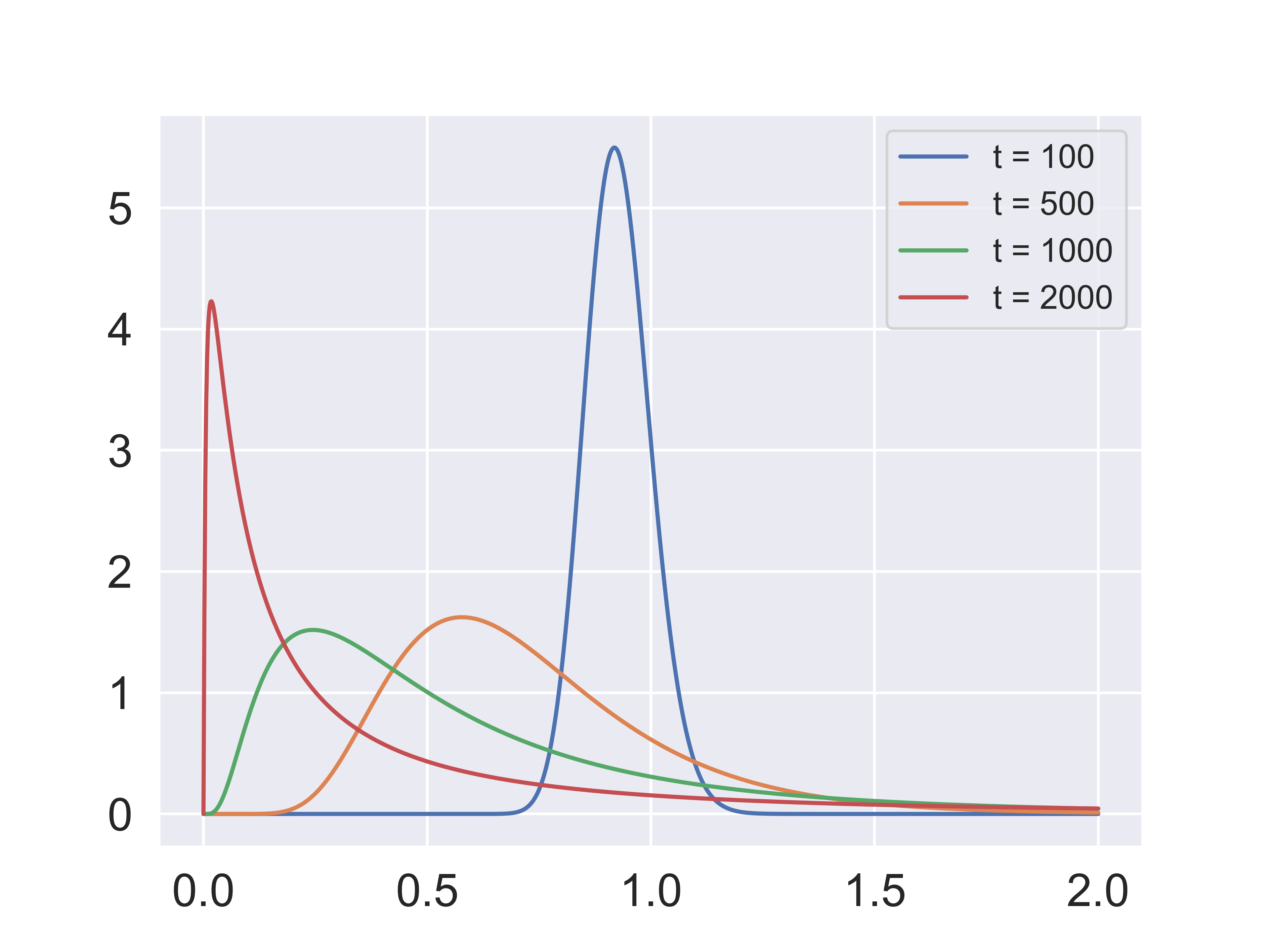
Fig. 7.2 Density of \(\widetilde{L}_t\) for different values of \(t\).#
Remark 7.7
Consider a positive cumulative return process, \(R,\) modeled as a stochastic functional. As we noted previously, for such a process, \(R_t/R_\tau\) for \(\tau < t\) is a \(t - \tau\)-period return for any such \(t\) and \(\tau\). Consider also the associated cumulative stochastic discount factor process, \(S,\) which we also take to be a multiplicative functional. For this process, \(S_t/S_\tau\) for \(\tau < t\) is the \(t - \tau\)-period stochastic discount factor for any such \(t\) and \(\tau\). Normalize \(R_0 = 1\) and \(S_0 = 1\). Repeating what we stated previously, by standard asset pricing logic, SR is a multiplicative martingale. [Martin, 2012] studies tail behavior of cumulative returns. Since its date zero conditional expectation is one, for long horizons this process necessary has a fat right tail as illustrated by Fig. 7.2.
While the multiplicative martingale has peculiar sample path properties, we are primarily interested in this martingale component as a change of probability measure. For instance, in Example 7.7, formula (7.13) for \({\widetilde N}_t\) tells how the change in probability measure induces mean \( {\mathbb H}\) in the conditional distribution for the shock \(W_{t+1}\). Similarly, \({\widetilde {\mathbb L}},\) with entries given in formula (7.10), provides an alternative transition matrix in Example 7.6.
7.5. Stochastic stability#
Our characterization of a change of probability measure as the solution of a Perron-Frobenius problem determines only transition probabilities. Since the process is Markov, it is of interest to seek an initial distribution of \(X_0\) under which the process is stationary and satisfies a stochastic stability property that we will define and explore. Stochastic stability opens the door the study of a variety of limiting behavior and hence justifies our interest in the multiplicative factorization. The eigenfunction problem can have multiple solutions, it turns out, however, that there is a unique solution for which the process \(X\) is stochastically stable under the implied change of measure, in particular, the solution associated with the minimum eigenvalue. See [Hansen and Scheinkman, 2009] and [Hansen, 2012] for formal analyses of this problem in a continuous-time Markov setting.
In what follows we investigate the discrete-time counterpart to their investigations.
Definition 7.3
A process \(X\) is stochastically stable under a probability measure \({\tilde {P}}\) if it is stationary and \(\lim_{j \rightarrow \infty} {\widetilde {\mathbb E}} \left[h(X_j) \mid X_0 = x \right] = {\widetilde {\mathbb E}} \left[ h(X_0) \right]\) for any Borel measurable \(h\) satisfying \({\widetilde E} \vert h(X_t) \vert < \infty\).
Theorem 7.2
Let \(M\) be a multiplicative functional. Suppose that \((\tilde \eta, \tilde e)\) solves the eigenfunction problem and that under the change of measure \(\widetilde P\) implied by the associated martingale \(\widetilde M\) the stochastic process \(X\) is stationary and ergodic. Consider any other solution \((\eta^*, e^*)\) to eigenfunction problem with implied martingale \(\{ M_t^* \}\). Then
\(\eta^* \ge \tilde \eta\).
If \(X\) is stochastically stable under the change of measure \(Pr^*\) implied by the martingale \(M^*\), then \(\eta^* = \tilde \eta\), \(e^*\) is proportional to \(\tilde e\), and \(M^* = \widetilde M\) for all \(t=0,1,... \).
Proof
First we show that \(\eta^* \ge \tilde \eta\). Write:
Thus,
If \(\tilde \eta > \eta^*\), then
But this equality cannot be true because under \(\widetilde{Pr}\) \(X\) is stochatically stable and \(\frac {e^*}{\tilde e}\) is strictly positive. Therefore, \(\eta^* \ge {\tilde \eta}.\)
Consider next the case in which \(\eta^* > \tilde \eta\). Write
which implies that
Thus,
Suppose that \(\tilde \eta < \eta^*\), then
so that \(X\) cannot be stochastically stable under the \(Pr^*\) measure.
Finally, suppose that \(\tilde \eta = \eta^*\) and that \(\frac {\tilde e(x)}{e^*(x)}\) is not constant. Then
and \(X\) cannot be stochastically stable under the \(Pr^*\) measure.
Stochastic stability under the change of measure provides way to think about some interesting long-term approximations. Suppose that
Then
Since \(X\) is stochastically stable under \({\widetilde P}r\),
This limit justifies the Perron-Frobenius eigenvalue as the long-term growth or decay rate of the multiplicative functional.
As we have mentioned previously, cumulative returns and cumulative stochastic discount factor processes can often be measured, conveniently, by multiplicative functionals. Suppose that
In the case of a cumulative return process, the implied \({\tilde \rho} > 0\) is the long-term logarithm of the expected return on the corresponding investment. The division by \(j\) in (7.15) adjusts for the horizon of the expected return. For a cumulative stochastic discount factor process, the resulting \({\tilde \rho} < 0\) is the negative of the yield on a long-term discount bond.
Under the restriction, after adjusting for the growth or decay in the semigroup, we obtain a more refined approximation:
where we assume that \({\widetilde {\mathbb E}}\left[{\frac {f(X_t)} {{\tilde e}(X_t)}}\right] < \infty\). Once we adjust for the impact of \({\tilde \eta}\), the limiting function is proportional to \({\tilde e}\). The function \(f\) determines only a scale factor \({\widetilde {\mathbb E}}\left[{\frac {f(X_t)} {{\tilde e}(X_t)}}\right] \tilde e(x)\).
We will apply the limiting results in a variety of ways in this and subsequent chapters. The multiplicative factorization can help us understand implications of stochastic equilibrium models for valuations of random payout processes. In addition, such factorizations can help organize empirical evidence in ways that make contact with such stochastic equilibrium asset pricing models.
7.6. Inferences about permanent shocks#
Macroeconomists often study dynamic impacts of shocks to systems of variables measured in logarithms. For example, [Alvarez and Jermann, 2005] suggest looking at asset prices using a multiplicative representation of a cumulative stochastic discount factor, though without the tools provided by this chapter. The additive decomposition derived and analyzed in Chapter 4 is a convenient tool for models like theirs.
We start with a factorization of a stochastic discount factor process as given in Theorem 7.1.
Take logarithms and form:
This looks like an additive decomposition of the type analyzed in Chapter 4, but it is actually different. While \(L^s\) is a multiplicative martingale, \(\log L^s\) is typically a super martingale, but not a martingale. This leads us to write the additive decomposition as:
where \({\widehat L}^s\) is an additive martingale. As [Hansen, 2012] argues, a weaker result holds. If \(L^s\) is not degenerate (i.e., equal to one), then \({\widehat L}^s\) is not degenerate and conversely. A prominent multiplicative martingale component implies a prominent role for permanent shocks in the underlying economic dynamics. A formal probability model lets us link the two representations via the results we have described in this chapter and Chapter 4. Log normal models, at least as approximations, are often used by applied macroeconomists. Example 7.7 provides an example with explicit formulas linking the two representations. While distinct, the two martingales, in this special case, are closely linked. In general, this simplicity vanishes, unfortunately.
7.7. Observable counterparts to a factorization of stochastic discount factors#
Consider stochastic discount factorization (7.16) again. A date zero price of a long-term bond is:
Compute the corresponding yield by taking \(1/t\) times minus the logarithm:
Provided that
the limiting yield on a discount bond is \(- \eta^s,\) as we noted previously.
Next consider a one-period holding period return on a \(t\) period discount bond:
Using stochastic stability and taking limits as \(t\) tends to \(\infty\) gives the limiting holding-period return:
A simple calculation shows that \(R_1^{\infty}\) satisfies the following equilibrium pricing restriction on a one-period return:
These long-horizon limits provide approximations to the eigenvalue for the stochastic discount factor and the ratio of the eigenfunctions. In a model without a martingale component [Kazemi, 1992], observed that the inverse of this holding-period return is the one-period stochastic discount factor. [Alvarez and Jermann, 2005] extend this insight by showing that the reciprocal reveals the component of one-period stochastic discount factor net of its martingale component.
Remark 7.8
Within the [Kazemi, 1992] setup, \((R_1^\infty)^{-1}\) equals the one-period stochastic factor. Let \(Y_1\) be a vector of asset payoffs and \(Q_0\) is a vector of corresponding prices. Then
Take the baseline probability measure to the data generating process as is often done under rational expectations. We may sidestep measuring this baseline probability by using the approach delineated by [Hansen and Singleton, 1982] and [Hansen and Richard, 1987] and converts our generalization of Kazemi’s insight into a testable restriction using generalized method of moments. See [Hansen, 1982].
Notice that rational expectations is imposed empirically under partial information, as it often is for Euler equation methods. This is very distinct from imposing rational expectations as an outcome determined by a fully-specified model. This full information approach can be imposed without feeding back on data. The expectations are model implied. Indeed many applied theory contributions embrace this approach to rational expectations. With the full information approach, maximum likelihood estimation and testing can be done as a second step in the analysis, as is featured in research by Sargent and others. See, for instance, the methods described in [Hansen and Sargent, 1980].
Within the [Kazemi, 1992] setup, a subjective belief specification as multiplicative martingale expressed in terms of a baseline probability specification could rationalize the martingale component of a cumulative stochastic discount factor process and capture the empirical failure using the approach just described. Thus the distinction between probability measures can be sufficient to induce a martingale component relative to baseline probabilities even though this component is absent when valuations are depicted with the subjective probabilities.
In practice, we have only have bond data with a finite payoff horizon, whereas the characterizations [Kazemi, 1992] and [Alvarez and Jermann, 2005] use bond prices with a limiting payoff horizon. Empirical implementations using such characterizations assume that the observed term structure data have a sufficiently long duration component to provide plausible proxy for the limiting counterpart.
7.8. Values of stochastic cash flows#
In a fundamental paper, [Rubinstein, 1976] featured the importance of cash-flow pricing in contrast to the often studied return-based analyses.
7.8.1. Finite-versus infinite valued claims#
In a recent paper, [Panageas, 2025] reminds us that several important issues that bear on finite values of equilibrium cash-flows including consumption. These issues include speculative bubbles, dynamic efficiency, and equity claims linked to macroeconomic outcomes. Importantly, he argues that the adjustment for uncertainty can play an important and sometimes subtle role in such evaluations.[1]
We explore when equity claims are finite by building stochastic counterparts to well known and pedagogically revealing Gordon growth model posed in discrete time. By using the framework developed in this chapter, we characterize the uncertainty adjustments necessary for such valuations. In so doing, we show how tools featured in Black-Scholes style option-pricing type analyses must be altered in important ways to understand these valuations.
We start by constructing the multiplicative functional using the product, \(M = G S,\) where \(G\) captures stochastic growth in the cash flow and \(S\) stochastic discounting. The factorization in Theorem 7.1 and the selection we featured in Theorem 7.2 provide a defense for using \(\tilde \eta\) as an asymptotic growth or decay rate of \(M\) provided that we select the solution that is stochastically stable. To justify finite values of equity-based assets for a family of cash flows, we restrict \(\tilde \eta<0\) so that stochastic discounting dominates stochastic growth. We now revisit that analysis, deconstruct the outcome, and explore the limitations.
7.8.1.1. Constant discounting#
As a warm-up, consider a discrete-time Gordon growth model where:
with \(\eta_s <0\) reflecting discounting and \(\eta_g\) capturing growth. The well known and simple to compute outcome gives:
for \(M = SG\), provided that \({\tilde \eta} = { \eta}_s + {\eta}_g < 0\). Thus we have the familiar restriction that discounting has to dominate growth in a deterministic setting.
As is also well-known, the separation is not quite so simple because growth contributes to the rate of return used for discounting. The term \({\tilde \eta}_s\) could reflect both subjective discounting in preferences and an adjustment contributed by economic growth in consumption that can either enhance or diminish the discount rate depending on investor preferences for intertemporal substitution.
7.8.1.2. Expected discounted cash flows#
Next consider discounted expected values for a \(\tilde \eta < 0 \) and a stochastically stable Markov process \(X\). Recall that stochastic stability implies that conditional expectations converge to their unconditional counterpart. Thus we, temporarily, abstract from uncertainty adjustments in valuation not reflected in conditional expectations or encoded in the discount rate. (We will be agnostic for how we come up with \(\tilde \eta\).) Consider the valuation of a positive claim on the Markov state say \(\phi(X),\)
Under the presumed stochastic stability of the Markov process, there are two possibilities are of interest:
While it is common to feature the finite-moment case, here we proceed more generally. Except for the finite-state Markov case, we may easily construct payoffs that are positive functions of the Markov state that have infinite expectations. When the unconditional expectation is infinite, the value of the equity-type claim may or may not be finite. In effect, there is a race between how fast the expectation diverges versus the magnitude of the discount rate \(- {\tilde \eta}\). When the former grows faster than \(- {\tilde \eta},\) the valuation in (7.18) will be infinite, even though the underlying Markov is stochastically stable.
Our more general approach required that we address a multiplicity that emerges when we factor \(M\). Take \(M_t =
\exp\left( \tilde \eta t \right) \phi(X_t).\) For sake of discussion, take \(S_t = \exp\left( \tilde \eta t\right)\), and \(G_t = \phi(X_t)\).
As a special case for such an \(M\) process, consider the solutions to the following equation:
Setting \({\hat e} = 1\) and \({\hat \eta} = 0\) solves this equation, but there can be other solutions. For such solutions, \( \hat \eta > 0,\) the conditional expectations will diverge geometrically, and they must have infinite unconditional moments. More generally, the potential divergence of the conditional moments is precisely the source of multiple factorizations for \(M,\) and what drives our choice of selecting one. The associated cash flow with a date \(t\) contribution, \(\phi(X_t) = {\hat e}(X_t),\) will have Infinite value when \(\hat \eta > - {\tilde \eta}\).
Example 7.9
Consider a special case of Example 7.8 with \(\nu = {\sf f}_1 = {\sf f}_2 =0. \) This makes \(M=1\). We look for solutions of the form:
The quadratic equation of interest simplifies to:
This has two solutions. One is \(\epsilon_2 = 0.\) For this one, \({\hat \eta}=0\) and \({\hat e} = 1\) and gives rise to the solution that we expect. For the other one,
\(\epsilon_1 = 0\), and
since \({\sf a}^2 < 1\).
7.8.1.3. A simple stochastic extension of the Gordon growth model#
To model stochastic growth and discounting, consider the very special case of two correlated geometric random walks with constant expected discounting or growth rates. Suppose
where \(\mu_s\) and \(\mu_g\) are constants with \(\mu_s < 0,\) \(\mu_g > 0\), and \(\sigma_s\) and \(\sigma_g\) are constant row vectors and the \(W\) process is iid with \(W_{t+1}\) being a multivariate standard normally distributed random vector. Form the product process, \(M = SG,\) which will have the same mathematical structure:
Construct
The first term in the second line captures the implied risk-free rate of the return, the second term the expected growth rate, and the third term, \(\sigma_s \cdot \sigma_g,\) includes an adjustment for uncertainty. The security with cash flow \(G\) has finite value when \(\tilde \eta < 0\) with the familiar geometric summation formula:
This computation illustrates a way to build a stochastic version the Gordon growth model, but it has important limitations from both a conceptual and empirical perspective.
7.8.1.4. Adjusting for uncertainty II#
The stochastic example in the previous subsection has pedagogical value, but the interest rates are constant as are the cash-flow growth rates. The same is true for the one-period cash-flow exposures to the shock vector \(W_{t+1}\). We escape this straight jacket by introducing state dependence expressed as follows:
By using the factorization of Theorem 7.1 and the unique selection of such a representation, Theorem 7.2, we return to our initial present-value analysis in [Subsection 7.8.1.2]:Expected discounted cash flows. Write
Consider a family of cash flows of the form
for different \(\phi\)’s. Stated in terms of logarithms, the cash-flows are all co-integrated (with co-integration coefficients one and minus one). The process \(G\) reflects a common stochastic growth component. [Hansen, 2012] explores in detail relations between co-integration as it is studied in macroeconomics and long-term valuation as it is of interest in this chapter. Distinct moment implications are made for both applications.
The uncertainty-adjusted valuation of the discounted cash flows of the form given in (7.20) is given by:
where the expectation uses the probability distribution induced by \({\widetilde E}\). Analogous to our initial computation, if \(\tilde \eta < 0\) and the unconditional moment
then the valuation will be finite. Notice that expectation of interest is for the ratio, \(\phi(X_t)/{\tilde e}(X_t),\) showing a role for the eigenfunction. Infinite values will arise whenever \({\tilde \eta} \ge 0.\) Thus \({\tilde \eta}\) as a measure of the asymptotic growth or decay in \(SG,\) plays a central role in determining whether the discounted expected value of the cash-flow \(G\) is finite or not. But like the analysis in [Subsection 7.8.1.2]:Expected discounted cash flows, there is a nuanced case in which
For this infinite-moment case, whether the discounted expected value is finite or not, depends on the rate of divergence in comparison to \(- {\tilde \eta}\).
Importantly, this analysis uses a change in probability measure for the computation. The change of measure imitates mathematically the familiar risk-neutral probability, but it is conceptually distinct. It depends on the stochastic behavior of \(SG\) and not just \(S\). Moreover, state-dependent short-term interest rates alone make the risk-neutral probabilities not the relevant one for valuing long-term cash flows. With state-dependence in stochastic growth, it becomes valuable to move from \(S\) to \(SG,\) which builds on the Gordon-growth insight. The uncertainty adjustments for valuation depend on the implied asymptotic rate of growth or decay, \(-{\tilde \eta},\) analogous to what happens in deterministic environments. It could, however, also depend on the corresponding behavior of the conditional expectations,
of the cash flows as the payoff horizon becomes large.
Although stated in the context of a very special example with specialized calculations, the analysis in [Panageas, 2025] reminds us that in a stochastic setting, unconditional moments can be infinite even when there is stochastic stability in the Markov process and the horizon-dependent conditional moments are finite. This means the value comparison for stochastic cash-flows with different specifications of \(\phi\) could be dramatically different because of the tail behavior of the stationary distributions of random variables \(\phi(X_t)/{\tilde e}(X_t)\) for the different \(\phi\)’s. More than the rate \({\tilde \eta}\) may come into play. It would appear to be hard to tell how restrictive the finite moment condition is empirically, but that does not mean we should dismiss it as a possibility. It sometimes matters when we build explicit models of valuation as illustrated by [Panageas, 2025].
7.8.2. Long-term risk-return tradeoff for cash flows#
Following [Hansen and Scheinkman, 2009] and [Hansen et al., 2008], we consider the valuation of stochastic cash flows, \(G\), that are multiplicative functionals. Such cash flows are determinants of prices of both equities and bonds.
We now study long-term limits of prices of such cash flows. In addition to the stochastic discount process (7.16), form:
with a corresponding cash-flow return over horizon \(t\):
Note that as a special case, the cash-flow return on a unit date \(t\) cash-flow is:
Define the proportional risk premium on the initial cash-flow return as the ratio of the expected return divided by the riskless counterpart for the same horizon. Taking logarithms and adjusting for the time horizon gives:
where the first term is the logarithm of the expected payoff, the second term is minus the logarithm of the price, and the third term is minus the logarithm of the riskless cash-flow return for horizon \(t\). Scaling by \(1/t\) adjusts for the investment horizon.
The product \(SG\) is itself a multiplicative functional. Let \(\eta^{sg}\) denote its geometric growth component. Then from (7.21), the limiting cash-flow risk compensation is:
This expression resembles the negative of covariance as is often found in asset pricing, but it differs from a covariance because we are working with proportional measures of the risk compensations.
We also investigate the limiting behavior of one-period holding period returns. An empirical asset pricing literature has explored these returns starting with [van Binsbergen et al., 2012]. See [Golez and Jackwerth, 2024] for a recent update of this evidence. Use the factorization of \(SG\) to get
Based as it is on a multiplicative factorization of \(SG\), this typically does not tell the difference between the logarithm of the factorization of \(S\) and the logarithm of the factorization of \(G\). We provide a characterization of the limiting one-period holding period return for the cash flow by imitating and extending our analysis of a limiting holding-period return for riskless bond. This gives the following cash-flow analogue to (7.17):
for the long-horizon cash flow holding period return. The eigenvalue and eigenfunction adjustments come from studying \(SG\) instead of \(S\). The limiting holding-period return now inherits a stochastic growth term \(G_1/G_0\). By multiplying this return by \(S_1/S_0\) we obtain \(N_1^{sg}\), the date one martingale increment for \(SG\). The one-period pricing relation for the cash-flow holding-period return follows immediately.
Finally, suppose that \(L^s = 1\) so that the martingale component of the stochastic discount factor process is degenerate. Then \(SG\) inherits the martingale component of \(G\), implying that
As a consequence, the long-term risk-return tradeoff is zero, since in the limit proportional risk compensation is
Thus when the stochastic discount factor process fails to have a martingale component, the long-term, risk-return tradeoff is degenerate.
7.9. Bounding investor beliefs#
We use the cumulative stochastic discount factorization to analyze two distince approaches to drawing inferences about investor beliefs.
7.9.1. Subjective beliefs in the absence of long-term risk#
Suppose that we have data on prices of one-period state-contingent claims. We can use these data to infer the one-period operator, \({\mathbb M}.\) Recall that we represent this operator using a baseline specification of the one-period transition probabilities. One possibility is that the one-period baseline transition probabilities agree with the data generation. Rational expectations models equate transition probabilities to those used by investors. More generally, investors could have subjective beliefs that can differ from the baseline specification:
investors think there are no permanent macroeconomic shocks;
investors don’t have risk-based preferences that can induce a multiplicative martingale in a cumulative stochastic discount factor process.[2]
Under these two restrictions, we could identify the \(L^s\) as the likelihood ratio for investor beliefs relative to the baseline probability distribution. Thus, the implied martingale component in the cumulative stochastic discount factor identifies the subjective beliefs of investors. Using this change of measure, the limiting long-term risk compensations derived in the previous section are zero. These assumptions allow for the “Ross recovery” of investor beliefs.[3]
7.9.2. Restricting the martingale increment with limited asset market data#
Initially, suppose we impose rational expectations by endowing investors with knowledge of the data generating process. With limited asset market data we cannot identify the martingale component to cumulative stochastic discount factor process without additional model restrictions. We can, however, obtain potentially useful bounds on the martingale increment. For some applications, in addition to that of [Alvarez and Jermann, 2005], [Bakshi and Chabi-Yo, 2012], see [Koijen et al., 2010]and [Lustig et al., 2019], among others. We know that as a stochastic process the implied martingale has some peculiar behavior and the martingale and transient components can be correlated. Nevertheless, the implied probability measure can be well behaved. Consequently, in contrast to the references just cited, we use the increment as a device to represent conditional probabilities instead of just as a random variable. Extensions of these same methods can be used to study restrictions on subjective beliefs implied by asset prices.
There is a substantial literature on divergence measures for probability densities. Relative entropy is an important example. More generally, consider a convex function \(\phi\) that is zero when evaluated at one. Jensen’s inequality implies that
and equal to zero when \(N_1\) is one, provided that \(N_1\) is a multiplicative martingale increment (has conditional expectation one). This gives rise to a family of \(\phi\) divergences that can be used to assess departures from baseline probabilities. Relative entropy, \(\phi(n) = n \log n\) is an example that is particularly tractable and has been used often. Both \(n \log n\) and \(- \log n\) can be interpreted as expected log-likelihood ratios.
One way of assessing the magnitude of the martingale increment to the stochastic discount factor is to solve:
Minimum divergence Problem
subject to:
where \(Y_1\) is a vector of asset payoffs and \(Q_0\) is a vector of corresponding prices, and where \({\widehat S_1}/{\widehat S_0}\) is equal to one of the two possibilities:
i) \(\exp(\eta^s) \frac{ e^s(X_0)} {e^s(X_1)}\) under under the data generating process;
or
ii) an imposed stochastic discount factor allowing for subjective beliefs to differ from the data generating process.
\noindent I regards to i), recall that the term
can be approximated by the reciprocal of the one-period holding-period return on a long-term bond. In regards to ii), for a model that is misspecified under the data generating process, we can ask that the distortion induced by the subjective beliefs correct the misspecification under the data generating process.
Remark 7.9
It is revealing to extend problem (7.22) to include an inequality constraint requiring that the conditional expectation of any random variable of interest be less than or equal to some threshold. Adding a constraint, when it binds, increases the objective. A given increase in the divergence is achieved by reducing this threshold sufficiently far. By following this procedure, we may find the lower bound on the moment of interest that increases the objective by some pre-specified percentage. Extending this approach to any bounded random variable reveals an ambiguity-induced nonlinear expectation operator, where the nonlinearity follows from our construction of a lower bounds on conditional expectations. To obtain an ambiguity interval for a given random variable follows from also constructing the lower bound for the negative of this random variable. See [Chen et al., 2020] for a more extensive discussion. Such a constructions are an example of what econometricians describe as partial identification because the vector \(Y_1\) of asset payoffs used in the analysis may not be sufficient to reconstruct all potential one-period asset payoffs and prices. In effect, the econometrician is often confronted with incomplete data on financial markets.
Remark 7.10
Many researchers use \(\phi(n) = - \log n\) as a divergence measure. [Chauduri et al., 2023] and [Chen et al., 2024], however, isolate a potentially problematic aspect of monotone decreasing divergences such as \(- \log n\) because they can fail to detect certain limiting forms of deviations from baseline probabilities.
Remark 7.11
[Ghosh and Roussellet, 2023] suggest a formal econometric procedure for estimating the minimum divergence altered probability measure using conditioning information. Presumably their methods could be extended to produce conditional ambiguity intervals as well.
Remark 7.12
To avoid having to estimate conditional expectations, applications often study an unconditional counterpart to this problem. In such situations, conditioning can be brought in through the “back door” by scaling payoffs and prices with variables in the conditioning information set; for example, see [Hansen and Singleton, 1982] and [Hansen and Richard, 1987]. See [Bakshi and Chabi-Yo, 2012] and [Bakshi et al., 2017] for some related implementations.
Remark 7.13
[Alvarez and Jermann, 2005] use \(- {\mathbb E}\left( \log S_1 + \log S_0 \right) \) as the objective to be minimized. Notice that
where the term in square brackets is the logarithm of the reciprocal of the limiting holding-period bond return. The criterion thus equals that in the minimum divergence problem, but with an additive translation. Rewrite the constraints in the minimum divergence problem as:
Thus we are left with an equivalent minimization problem in which the translation term is subtracted off to obtain the bound of interest.
Applied researchers have sometimes omitted the first constraint, which weakens the bound.
7.9.2.1. Intertemporal divergence measures#
[Chen et al., 2020] propose extensions of the one-period divergence measures to multi-period counterparts that remain tractable and enlightening. By looking over time, the dynamic formulation essentially averages over the conditioning information; but it allows for subjectivity in the transition probabilities. Their dynamic measure of divergence is constructed as follows. For a given \(N\) process, let
As we have seen, this construction provides the implied transition probability adjustments for the alternative time horizons. Find a function \(\psi\) such that
With these inputs form an alternative equivalent way to represent the one-period divergence by constructing a function \(\psi\) such that
The function \(\psi\) plays a role analogous to \(\phi\) when the roles between the \(N\)-implied probability and the baseline probability are interchanged. It may be shown that \(\psi\) also strictly convex. Note also that \(\psi(1) = \phi(1) = 1\). By design,
With these building blocks, [Chen et al., 2020] suggest the divergence measure:
An alternative equivalent representation may be obtained by taking a Law of Large Numbers limit under the altered probability measure. When \(\phi(n) = n \log n,\) this divergence measure coincides with the one that is pertinent for the study of Donsker-Varadhan formulations of large deviations in Markov environments. Our interest here is different as the this dynamic formulation of divergences opens the door to a dynamic recursive constructions of the bounds in the divergence minimization described in Remark 7.9.
7.9.2.2. Subjective belief bounds on proportional risk premia#
The next two figures report proportional risk compensations for the market return using an illustration from [Chen et al., 2020] under a presumed data generation and when distorted investor beliefs are permitted and risk aversion is constrained to be one. The compensations condition on dividend/price ratios. The figures includes upper and lower endpoints of conditional expectations computed by extending the divergence minimization problem along the lines suggested Remark 7.9 given by the upper and lower edges of shaded rectangles. The horizontal lines within the shaded rectangles given the conditional moments implied by the minimum divergence change in probability measure. By comparing the two figures, we see how the ambiguity intervals decrease when we weaken the constraint on the divergence. Since the divergence measure used in the computation is explicitly dynamic, the corresponding subjective probabilities for the transition probabilities are also substantially altered. The implied stationary probabilities for the three states are
Notice that the altered probabilities reflect a substantial reduction of being in the high dividend-price state, making the big conditional divergence for the high dividend-price state perceived to be less impactful on the dynamic divergence measure.
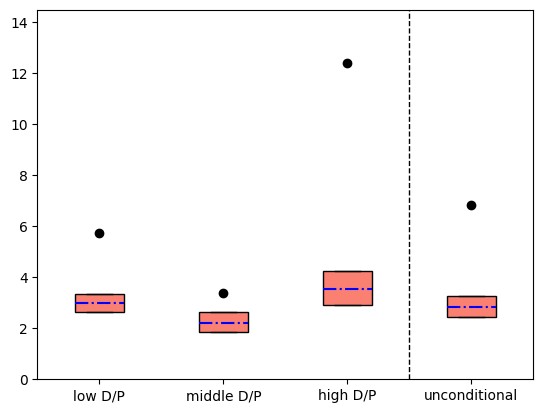
Fig. 7.3 Proportional risk compensations computed as \(\log \mathbb{E} R^m - \log \mathbb{E} R^f\) scaled to an annualized percentage. The \(\bullet\)s are the empirical averages and the boxes give the imputed bounds when we inflated the minimum relative entropy by 20%.#
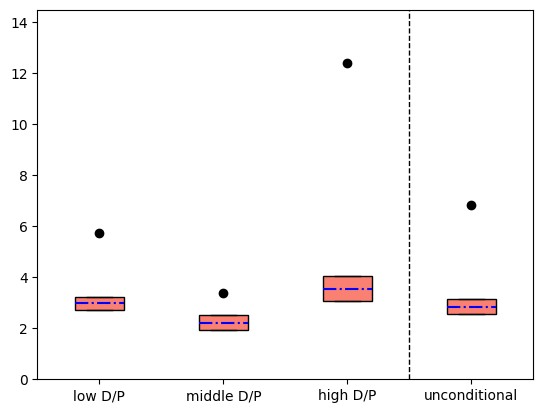
Fig. 7.4 Proportional risk compensations computed as \(\log \mathbb{E} R^m - \log \mathbb{E} R^f\) scaled to an annualized percentage. The \(\bullet\)s are the empirical averages and the boxes give the imputed bounds when we inflated the minimum relative entropy by 10%.#
