4. Processes with Markovian increments#
\(\newcommand{\eqdef}{\stackrel{\text{def}}{=}}\)
Chapter 3 described some implications of processes with stationary increments. In this chapter, we add structure by modeling the increments as a stationary Markov process. Such processes are commonly used to model economic time series of logs of key macroeconomic variables like GDP, capital and labor stocks, and price levels with stochastic growth that is additive over time. Eventually, we will explore the implications of exponentiating a process with stationary increment processes. Doing that transforms an arithmetically growing process to one that displays geometric stochastic growth.
4.1. Definition of additive functional#
Let \(\{W_{t+1} : t \ge 0\}\) be a \(k\)-dimensional stochastic process of unanticipated economic shocks. Let \(\{ X_t : t \ge 0 \}\) be a discrete-time stationary Markov process that is generated by initial distribution \(Q\) for \(X_0\) and transition equation
where \(\phi\) is a Borel measurable function. Let \(\left\{ \mathfrak{A}_t : t=0,1,... \right\}\) be the filtration generated by histories of \(W\) and \(X\); \(\mathfrak{A}_t\) serves as the information set (sigma algebra) generated by \(X_0, W_1, \ldots , W_t\). We presume that the conditional probability distribution for \(W_{t+1}\) conditioned on \(\mathfrak{A}_t\) depends only on \(X_t\). To assure that the process \(\{W_{t+1} : t \ge 0 \}\) represents unanticipated shocks, we restrict it to satisfy
We produce results that condition on a statistical model in the sense of Section Limiting Empirical Measures in Chapter 1:Laws of Large Numbers and Stochastic Processes, or equivalently on invariant events. Given this, for notational simplicity, we simply assume that the stationary \(\{X_t : t \ge 0\}\) process is ergodic.[1] The Markov structure of \(\{ X_t \}\) makes the distribution of \((X_{t+1}, W_{t+1}) \) conditioned on \(\mathfrak{A}_t\) depend only on \(X_t\).[2]
Definition 4.1
A process \(\{ Y_{t} \}\) is said to be an additive functional if it can be represented as
for a (Borel measurable) function \(\kappa: {\mathbb R}^n \times {\mathbb R}^k \rightarrow {\mathbb R}\), or equivalently
where we initialize \(Y_0\) at some arbitrary random variable depending on date zero information, although such a restriction is not needed for what follows.
Definition 4.2
An additive functional \(\{ Y_t : t=0,1,...\}\) is said to be an additive martingale if \(E\left[ \kappa(X_{t}, W_{t+1}) \vert X_t \right] = 0.\)
Note that \(E\left[ \kappa( X_t, W_{t+1} ) \vert X_t \right] = 0\) implies the martingale restriction that we used previously:
It is easy to see that a linear combination of two additive functionals \(\{Y_{t}^{[1]}\}\) and \(\{Y_{t}^{[2]}\}\) is itself an additive functional. If \(\kappa_1\) is used to construct the first process and \(\kappa_2\) the second process, then \(\kappa = \kappa_1 + \kappa_2\) can be used to construct the sum of the two processes. –>
Example 4.1
Suppose that
where \(\{ W_{t+1} : t\ge 0 \}\) is an i.i.d.~sequence of standardized multivariate normally distributed random vectors, \({\mathbb A}\) is a stable matrix, and \({\mathbb B}\) has full column rank, and the random vector \(X_0\) is generated by initial distribution \(Q\) associated with the stationary distribution for the \(\{ X_t \}\) process. Here \(\mu(X_t)\) is the conditional mean of \(Y_{t+1} - Y_t\) and \(|\sigma(X_t)|^2\) is its conditional variance. When \(\sigma\) depends on \(X_t\), this is called a stochastic volatility model because \(|\sigma(X_t)|^2\) is a stochastic process. Conditional variances evolve stochastically over time.
In Example 4.1, when the conditional mean \(\mu(X_t) = 0\), the process \(\{Y_t \}\) is a martingale.
4.2. Extracting Martingales#
We can decompose an additive functional into a sum of components, one of which is an additive martingale that encapsulates all long-run stochastic variation as in Proposition 3.1. In this section, we show how to extract the martingale component. We adopt a construction like that used to establish Proposition 3.1 and proceed in four steps.
4.2.1. Martingale construction#
Construct the trend coefficient as the unconditional expectation:
Form the random variable \(H_t\) by computing multiperiod forecasts for each horizon and summing these forecasts over all horizons. Start by constructing
Thus
Summing the terms, construct
where \({\mathbb T}\) is the operator defined in (2.1). The right side becomes a function of only \((X_{t-1},W_t)\) once we substitute for \(\phi(X_{t-1},W_t)\) for \(X_t\) as implied by (4.1).
This construction requires that the infinite sum
converges in mean square under the stationary distribution for \(\{X_t: t\ge 0\}\). A sufficient condition for this is that \({\mathbb T}^m\) is a strong contraction for some integer \(m \geq 1\) and \(\overline{\kappa} \in {\mathcal N}\) where \({\mathcal N}\) is defined in (2.7).
Compute
where[3]
Build the martingale increment:
where
By construction, the expectation of \(\kappa_m(X_t, W_{t+1})\) conditioned on \(X_t\) is zero.
Armed with these calculations, we now report a Markov counterpart to Proposition 3.1.
Proposition 4.1
Suppose that \(\{Y_{t} : t\ge 0\}\) is an additive functional, that \({\mathbb T}^m\) is a strong contraction on \({\mathcal N}\) for some \(m\), and that \(E[\kappa(X_{t},W_{t+1})^2] < \infty\). Then
Notice that the martingale component is itself an additive functional. The first is a linear time trend, the second an additive martingale, the third a stationary process with mean zero, and the fourth a time-invariant constant. If we happen to impose the initialization: \(Y_0 = - \kappa_+(X_0)\), then the fourth term is zero. We use Proposition 4.1 decomposition as a way to associate a ‘’permanent shock’’ with an additive functional. The permanent shock is the increment to the martingale.
4.3. Applications#
We now compute martingale increments for two models of economic time series.
4.3.1. Vector autoregression#
We apply the four-step construction in Algorithm Martingale construction when the Markov state \(\{ X_t \}\) follows a first-order VAR
where \({\mathbb A}\) is a stable matrix and \(\{ W_{t+1} : t\ge 0 \}\) is a sequence of independent and identically normally distributed random variables with mean vector zero and identity covariance matrix. The one-step ahead conditional covariance matrix of the time \(t+1\) shocks \(\mathbb{B} W_{t+1}\) to \(X_{t+1}\) equals \(\mathbb{B} \mathbb{B}'\). Let
where \({\mathbb D}\) and \({\mathbb F}\) are row vectors with the same dimensions as \(X_t\) and \(W_{t+1}\), respectively. For this example, the four steps of Algorithm Martingale construction become:
The trend growth rate is \(\eta\) as specified.
- \[\kappa_h(X_{t-1}, W_t, X_t ) = {\mathbb D} X_{t-1} + {\mathbb F} W_{t} + {\mathbb D}({\mathbb I} - {\mathbb A} )^{-1} X_t \]
- \[\kappa_+(X_t) = {\mathbb D} X_t + {\mathbb D} ({\mathbb I} - {\mathbb A} )^{-1}{\mathbb A} X_t = {\mathbb D}({\mathbb I} - {\mathbb A} )^{-1} X_t\]
- (4.6)#\[\begin{align} \kappa_m(X_{t-1}, W_t) & = {\mathbb F} W_{t} + {\mathbb D} ({\mathbb I} - {\mathbb A} )^{-1} (X_t - {\mathbb A} X_{t-1} ) \cr & = \left[{\mathbb F} + {\mathbb D} ({\mathbb I} - {\mathbb A} )^{-1} {\mathbb B} \right] W_t. \end{align}\]
From Example 1.8, we expect the coefficient of martingale increment to be the sum of impulse responses for the increment process \(\{ {\mathbb D} X_t + {\mathbb F} W_{t+1} : t\ge 0\}\). The impulse response function is the sequence of vectors:
Summing these vectors gives
as anticipated.
4.3.2. An economic rationale#
Recursive utility represents preferences using recursively-constructed continuation values. As an illustration, let \(V_t\) be the date \(t\) continuation value used to rank current and future consumption, and let \({\widehat V}_t\) denotes its logarithm. Suppose that for the logarithm of consumption, \({\widehat C}_t = \log C_t\),
where the first two equations are backward looking and third and fourth ones are forward looking. In particular, current \({\widehat V}_t\) depends on the future \({\widehat V}_{t+1}\) through the construction of \({\widehat R}_t.\) In turn, \({\widehat R}\) is risk-adjusted certainty-equivalent of the next period continuation value \({\widehat V}_{t+1}\). In particular, these preferences use an exponential risk adjustment as reflected in formula for \({\widehat R}_t\) instead of the conditional expectation of the future continuation value. We restrict the subjective discount factor, \(\beta,\) to satisfy \(0 < \beta < 1,\) and the risk aversion parameter, \(\gamma,\) to satisfy \(\gamma \ge 1.\) The \({\mathbb A}\) matrix governing the state dynamics is a stable. The forward equations typically require a terminal condition for the continuation value to be used in computing a solution for today’s continuation value iteratively. Here we impose time invariance by considering an infinite-horizon specification, one that could be constructed by taking a limit of finite horizon problems with zero terminal conditions.
These preferences are a special case of preferences [Kreps and Porteus, 1978] and [Epstein and Zin, 1989] for which feature a role for the intertemporal composition of risk. In the limiting case as \(\gamma \downarrow 1,\) \(R_t\) is the conditional expectation allowing us to write the continuation value recursion as:
which can be solved forward to obtain:
Thus this limiting case gives discounted expected logarithmic utility as a way to assess alternative consumption processes.
When the process \(\{ {\mathbb D} X_t\}\) is highly persistent, there is said to be substantial “long-run risk” in consumption. [Bansal and Yaron, 2004] also consider a process governing stochastic volatility that we abstract from in the computations that follow. While the illustrative calculations in what follows use the VAR-type application of [Hansen et al., 2008], some of the basic insights extend much more generally.
To provide a Markov characterization of the continuation value process, it is convenient to subtract \({\widehat C}_t\) from both sides of the second equation:
and rewrite the third equation as:
Given the assumed dynamics for the growth rate in consumption, \({\widehat C}\) and \({\widehat V}\) are co-integrated. We use ``guess and verify’’ to seek a solution of the form:
The coefficient vector \(\upsilon\) satisfies:
with a solution:
Notice that the formula for the coefficient \(\upsilon\) does not depend on the choice of \(\gamma\).
The scalar \({\sf v}\) satisfies:
where we have computed expectations using known calculations for log-normally distributed random variables.
Solving this forward gives:
Notice the first term in the square brackets of (4.8) is the average growth rate expressed in logarithms. For the second contribution, it is revealing to inspect the \(\beta = 1\) limit. Observe that the limiting version of \(\upsilon\) is:
implying that the term of interest is
This gives a variance adjustment to the continuation value that the product of \((1-\gamma)/2\) and variance of the increment to the martingale component of the logarithm of consumption as reported in (4.6). When \(\gamma = 1,\) this variance adjustment is zero. Larger values of \(\gamma > 0\) increases this adjustment. The \(\beta = 1\) limit is pertinent because this parameter is often set close to unity in the macro-finance literature.
As an illustration [Hansen et al., 2008] and [Hansen and Sargent, 2021], identify long-term risk in consumption by imposing cointegration on a VAR. By design, in what follows, we will abstract from model uncertainty and follow the common practice of plugging in estimates as if they were known with certainty. Later chapters will take the challenge of incorporating model uncertainty into preferences.
We construct a trivariate VAR system in which (1) the logarithm of proprietor’s income plus corporate profits, (2) the logarithm of personal dividend income, and (3) the logarithm of consumption have the same trend growth rate and martingale increment. Fig. 4.1 reports log differences in two time series.
Fig. 4.1 Time series for the i) logarithm of proprietor’s income plus corporate profits relative to consumption (blue) and ii) the logarithm of personal dividend income relative to consumption (red).#
We follow [Hansen and Sargent, 2021] by constructing a VAR system in the steps that follow:
Form:
where \(C_t\) is consumption, \(Bus_t\) is business income, and \(Div_t\) is personal dividend income.
Construct
Express a vector autoregression and consumption growth as;
where \({\mathbb A}\) is a stable matrix (i.e., its eigenvalues are all bounded in modulus below unity) and \({\mathbb B}{\mathbb B}'\) is the innovation covariance matrix. Similar constructions can be done for the growth in business income and in dividend income by using the formulas:
Thus both can be constructed as linear transformations of \(Z_{t+1}\) and \(Z_t\).
Deduce a common permanent shock to all three time series using the approach describe in Section Permanent shocks of Chapter Stationary Increments using formula
where
The initial scaling on the right side of the formula for the row vector, \({\mathbb F}^p,\) is done so that the permanent shock, \(W_{t+1}^p\), has standard deviation equal to one. We think of the shocks that are linear combinations of \(W_{t+1}\) formed with coefficient vectors that are orthogonal for \({\mathbb F}^p\) as being transitory. Their long-term impulse response is zero. They are not uniquely defined without further (potentially economic) restrictions. This lack of uniqueness is evident because there are multiple three-dimensional vectors that are orthogonal to \({\mathbb F}^p.\) Linear combinations of any orthogonal vectors are also orthogonal to \({\mathbb F}^p.\) There is two-dimensional subspace of such vectors.
We report the impulse responses of log consumption to the permanent shock and two transitory shocks in Fig. 4.2. All three shocks are normalized to have a unit standard deviation and the responses are multiplied by 100. Notice that the permanent shock has a substantial impact that builds over time. Its limiting value is \(|{\mathbb D} \left({\mathbb I} - {\mathbb A}\right)^{-1}{\mathbb B} + {\mathbb F} |\), which we verified contributes to the continuation value of consumption as reflected in (4.9).
The magnitude of the limiting version of this response is pertinent for the long-run risk model for the limiting case in which the subjective rate of discount is zero. Measure of long-term impacts can be challenging as we will see in the next chapter.
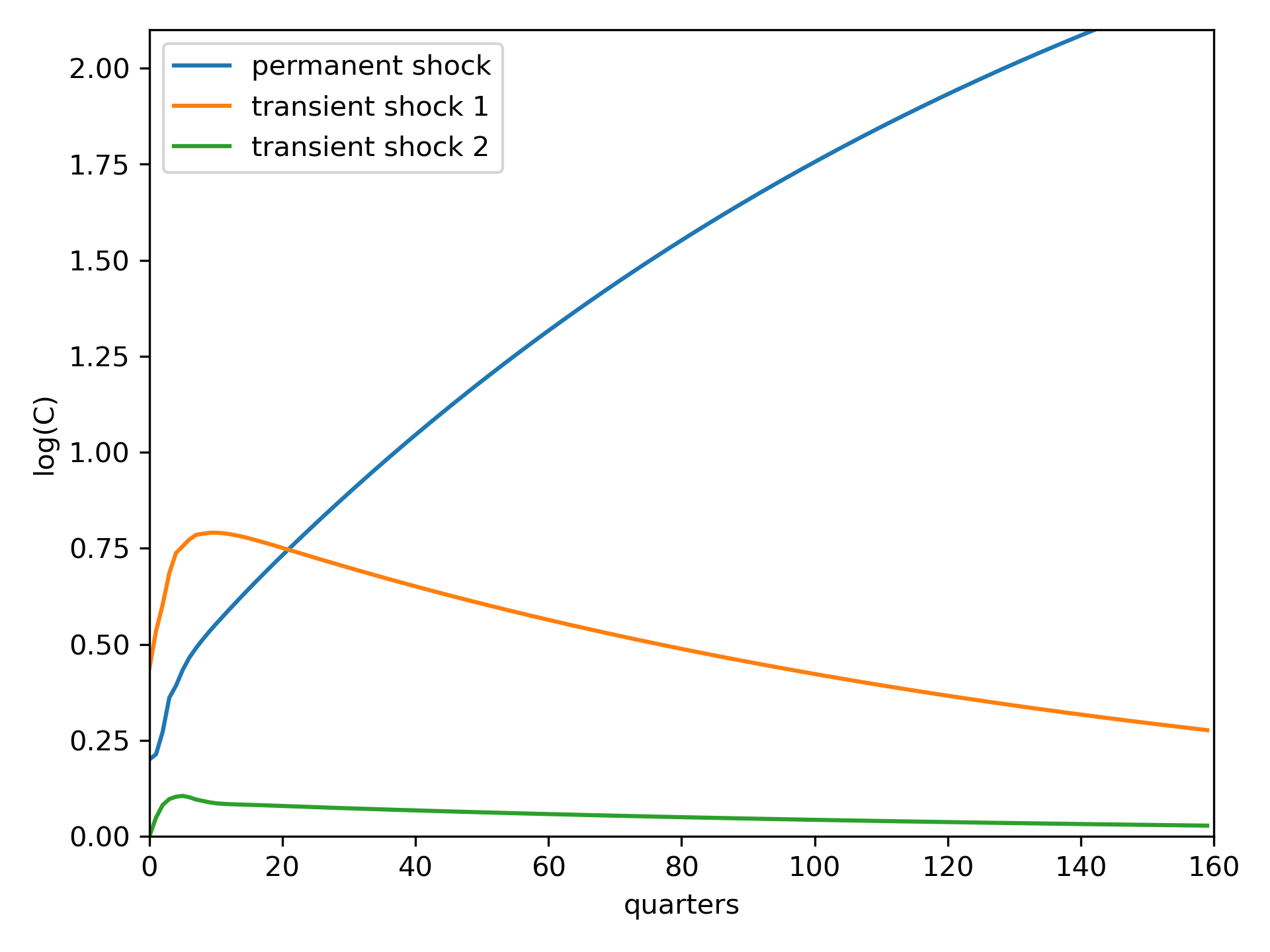
Fig. 4.2 Impulse responses of log consumption to permanent and two transitory shocks. The blue curve depicts the responses to a permanent shock. Responses to other transitory shocks are linear combinations of the two that are plotted.#
In Chapter 8:Exploring Recursive Utility, we investigate more generally the implications of a class of recursive utility preferences which nests this specification as a special case. Among other results, we obtain analogous formulas as first-order approximations to more general consumption dynamics.
4.3.3. Growth-Rate Regimes#
We construct a Proposition 4.1 decomposition for a model with persistent switches in the conditional mean and volatility of the growth rate \(Y_{t+1}- Y_t\).
Suppose that \(\{X_t : t \ge 0\}\) evolves according to an \(n\)-state Markov chain with transition matrix \({\mathbb P}\). Realized values of \(X_t\) are coordinate vectors in \({\mathbb R}^n\). Suppose that \({\mathbb P}\) has only one unit eigenvalue. Let \({\bf q}\) be the row eigenvector associated with that unit eigenvalue normalized so that \({\bf q} \cdot {\bf 1}_n = 1\) and
Consider an additive functional satisfying
where \(\{ W_{1,t} \}\) is an i.i.d. sequence of multivariate standard normally distributed random vectors. Evidently, the stationary Markov \(\{X_t : t \ge 0 \}\) process induces discrete changes in both the conditional mean and the conditional volatility of the growth rate process \(\{ Y_{t+1} - Y_t \}\).
Observe that \( E (X_{t+1} | X_t ) ={\mathbb P} X_t \) and let
Thus we can represent the evolution of the Markov chain as
\(\{W_{2,t+1} : t \ge 0 \}\) is an \(n \times 1\) discrete-valued vector process that satisfies \(E ( W_{2,t+1} | X_t) = 0 \), which is therefore a martingale increment sequence adapted to \(X_t, X_{t-1}, ..., X_0\).
We again apply the four-step construction in algorithm.[4]
- \[\eta = {\mathbb D} {\bf q} \]
- \[H_t = {\mathbb D} (X_{t-1} - {\bf q}) + {X_{t-1}}'{\mathbb F} W_{1,t} + {\mathbb D}\left({\mathbb I} - {\mathbb P}\right)^{-1} (X_t - {\bf q}) \]
- \[H_t^+ = E\left( H_{t+1} \mid X_t \right) = {\mathbb D} \left( X_{t} - {\bf q} \right) + {\mathbb D}\left({\mathbb I} - {\mathbb P}\right)^{-1} {\mathbb P}(X_t - {\sf q})\]
which implies that
\[\kappa_+(x) = {\mathbb D} \left( x - {\bf q} \right) + {\mathbb D}\left({\mathbb I} - {\mathbb P}\right)^{-1} {\mathbb P} \left(x - {\sf q}\right)\] - \[G_t = H_t - H_{t-1}^+ = {X_{t-1}}'{\mathbb F} W_{1,t} + {\mathbb D}\left({\mathbb I} - {\mathbb P}\right)^{-1} W_{2,t}\]
where we have substituted from equation (4.11).
The martingale increment has both continuous and discrete components:
