Notebook: Discrete Time#
Shock elasticities quantify the (local) exposures of macroeconomic cash flows to shocks over alternative investment horizons and the corresponding prices or investors’ compensations. Here we cover shock elasticities for models that are exponential-quadratic. This model structure is particularly tractable with quasi-analytical solutions.
Section 1 introduces the exponential–quadratic framework.
Section 2 provides an illustration using a long-run risk model.
Section 3 provides more details on the computation.
This notebook provides both written explanations and accompanying code. Please refer to the following papers for further details:
1. Exponential-linear-quadratic Framework#
We suppose a linear-quadratic specification of the state dynamics:
The code will take the coefficients as inputs.
Furthermore, we suppose that the logarithms of macroeconomic and stochastic discount factor processes that interest us grow or decay stochastically over time with stationary increments. Let \(Y\) be the logarithm of such a process. The process \(Y\) will display linear growth or decay:
Following the steps of our approximation of \(X\), we write
where \(\kappa_i\) is the derivative of \(\kappa\) with respect to argument \(i\) evaluated at \((\bar x, 0, 0)\) and similarly for the second derivatives.
In what follows, \(M\) will be a macro growth process, a stochastic discount factor process, or a product of the two. The user inputs are the quadratic specifications in equation (1) and equation (2).
We consider two types of multiplicative processes, one that captures macroeconomic growth, denoted by \(G\), and another that captures stochastic discounting, denoted by \(S\).
The stochastic discount factor process, \(S\), is typically computed from the underlying economic model to reflect equilibrium valuation dynamics.
For instance, the growth process \(G\) might be a consumption process or some other endogenously determined cash flow, or it might be an exogenously specified technology shock process that grows through time.
The interplay between \(S\) and \(G\) will determine uncertainty compensations over multi-period investment horizons.
Consider the pricing of a vector of payoffs \(G_tW_1\) in comparison to the scalar payoff \(G_t\).
The shock-exposure elasticity is constructed as from the ratio of expected payoffs \(E[G_tW_1 |X_0 =x]\) relative to \(E [G_t | X_0 = x]\). To calculate shock-exposure elasticity, the multiplicative functional \(M\) is set as \(G\).
\[ \varepsilon_{g}( x, t)= \frac{(\alpha_0 + \alpha_1 x) \cdot {\mathbb E}\left[\left( \frac {G_t}{G_0}\right) W_1 \mid X_0 = x\right]}{{\mathbb E} \left(\frac {G_t}{G_0} \mid X_0 = x\right)} \]This is done by the function _exposure_elasticity.
The shock-price elasticity includes an adjustment for the values of the payoffs \(E [S_t G_t W_1 | X_0 = x]\) relative to \(E [S_t G_t | X_0 = x]\). To calculate shock-price elasticity, the multiplicative functional \(M\) is set as the product \(SG\).
The shock-price elasticity is:
This computation is done by the function price_elasticity.
2. An Illustration using the Long-Run Risk Model#
We will now cover how to use the code on a basic level. You can see the package requirements here.
import os
import sys
workdir = os.getcwd()
!git clone https://github.com/lphansen/RiskUncertaintyValue
workdir = os.getcwd() + '/RiskUncertaintyValue'
sys.path.insert(0, workdir+'/src')
from IPython.display import display, HTML
display(HTML("<style>.container { width:97% !important; }</style>"))
import numpy as np
np.set_printoptions(suppress=True)
from scipy.stats import norm
import pandas as pd
import matplotlib.pyplot as plt
from numba import njit, prange
import seaborn as sns
from lin_quad import LinQuadVar
from lin_quad_util import next_period, log_E_exp, kron_prod, distance
from utilities import mat, vec, sym
from elasticity import exposure_elasticity, price_elasticity
fatal: destination path 'RiskUncertaintyValue' already exists and is not an empty directory.
We use the long-run risk model adapted from [Hansen et al., 2024] as an example; the model is outlined in Solving a planner’s problem with recursive utility. In a later lecture, you will learn how to solve such models using expansion methods. For now, suppose that we have solved the model and have the following linear-quadratic approximations for the states \(X_t = [X_{1,t},X_{2,t}]\) and consumption growth \({\widehat C}_{t+1} - {\widehat C}_t\):
First-order approximation:
Second-order approximation:
Note that the superscript refers to the approximation order and the subscript refers to the state. We store the approximations in objects of class LinQuadVar. For example, we can form the approximations described above as follows:
n_X = 2 #Two states
n_W = 3 #Three shocks
# State approximation where first row is X_1 and second row is X_2
X1_tp1 = LinQuadVar({'x': np.array([[0.9, 0. ],
[0. , 0.8]]),
'w': np.array([[0., 0.06, 0. ],
[0., 0. , 0.5]])},
shape=(2, n_X, n_W))
X2_tp1 = LinQuadVar({'x2': np.array([[0.9, 0. ],
[0. , 0.]]),
'xw': np.array([[0., 0., 0., 0., 0.06, 0. ],
[0., 0., 0., 0., 0. , 0.]])},
shape=(2, n_X, n_W))
### Log consumption growth
gc_tp1 = LinQuadVar({'c': np.array([[0.01]]),
'x': np.array([[0.03, 0.]]),
'w': np.array([[0.008, 0.01, 0.]]),
'x2': np.array([[0.01, 0.]]),
'xw': np.array([[0., 0., 0., 0.004, 0.01, 0.]])
}, shape=(1, n_X, n_W))
Next, we input these approximations into the exposure_elasticity function to compute exposure elasticities.
2.1 Exposure Elasticity for Consumption Growth#
To calculate the exposure elasticity for consumption growth using the exposure_elasticity defined above, we need six inputs
Consumption growth, gc_tp1. This is a LinQuadVar object.
First order expansion of the state evolution equations, X1_tp1. This is a LinQuadVar object.
Second order expansion of the state evolution equations, X2_tp1. This is a LinQuadVar object.
Time periods, \(\text{T} = 30\) years
Shock index, \(0\) stands for the growth shock, which means \(\alpha' =\begin{bmatrix}1 & 0 & 0 \end{bmatrix}\), \(1\) stands for the volatility shock, \(2\) stands for the consumption shock. The fourth shock alters dividend growth and its shock prices are zero.
Percentile, \(0.5\) stands for the median
## Calculate exposure elasticity for consumption growth
quantile = [0.1, 0.5, 0.9]
T = 30
expo_elas_shock_0_015 = [exposure_elasticity(gc_tp1, X1_tp1, X2_tp1, T, shock=0, percentile=p) for p in quantile] # The first shock is the growth shock
expo_elas_shock_1_015 = [exposure_elasticity(gc_tp1, X1_tp1, X2_tp1, T, shock=1, percentile=p) for p in quantile] # The second shock is the volatility shock
expo_elas_shock_2_015 = [exposure_elasticity(gc_tp1, X1_tp1, X2_tp1, T, shock=2, percentile=p) for p in quantile] # The third shock is the consumption shock
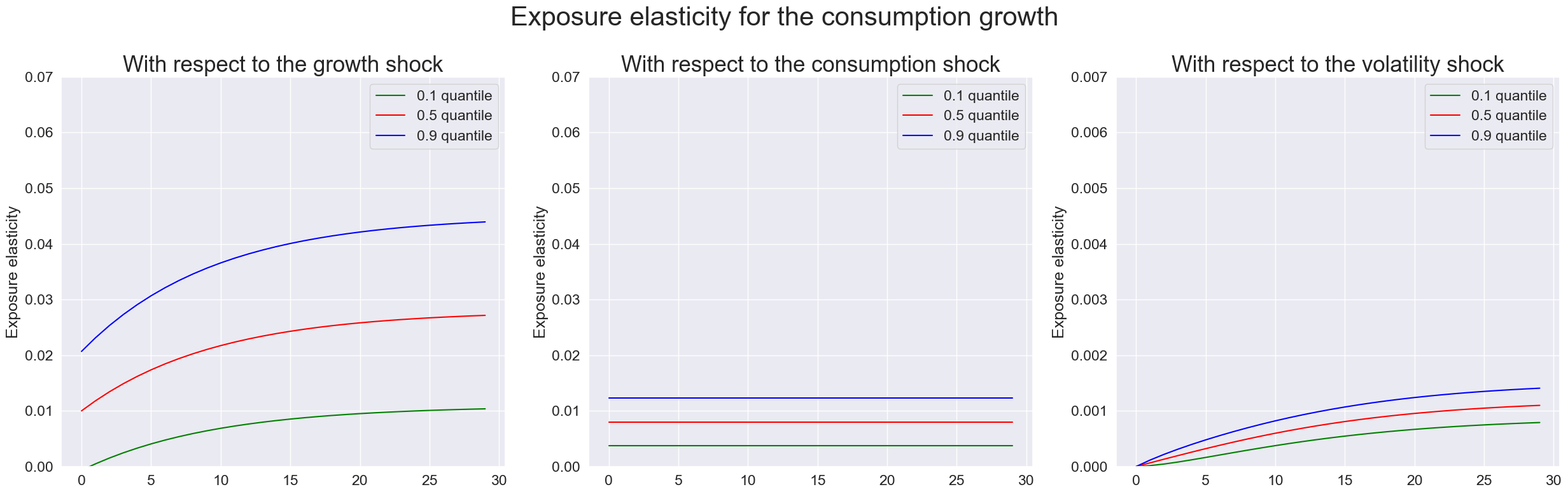
## Plot the exposure elasticity for consumption growth
index = ['T','0.1 quantile','0.5 quantile','0.9 quantile']
fig, axes = plt.subplots(1,3, figsize = (25,8))
expo_elas_shock_0 = pd.DataFrame([np.arange(T),expo_elas_shock_0_015[0].flatten(),expo_elas_shock_0_015[1].flatten(),expo_elas_shock_0_015[2].flatten()], index = index).T
expo_elas_shock_1 = pd.DataFrame([np.arange(T),expo_elas_shock_1_015[0].flatten(),expo_elas_shock_1_015[1].flatten(),expo_elas_shock_1_015[2].flatten()], index = index).T
expo_elas_shock_2 = pd.DataFrame([np.arange(T),expo_elas_shock_2_015[0].flatten(),expo_elas_shock_2_015[1].flatten(),expo_elas_shock_2_015[2].flatten()], index = index).T
n_qt = len(quantile)
plot_elas = [expo_elas_shock_1,expo_elas_shock_0, expo_elas_shock_2] # For illustration purpose, the consumption shock is plotted in the second column, the volatility shock is plotted in the third column
shock_name = ['growth shock', 'consumption shock', 'volatility shock']
qt = ['0.1 quantile','0.5 quantile','0.9 quantile']
colors = ['green','red','blue']
for i in range(len(plot_elas)):
for j in range(n_qt):
sns.lineplot(data = plot_elas[i], x = 'T', y = qt[j], ax=axes[i], color = colors[j], label = qt[j])
axes[i].set_xlabel('')
axes[i].set_ylabel('Exposure elasticity')
axes[i].set_title('With respect to the ' + shock_name[i], fontsize=25)
axes[2].set_ylim([0,0.007])
axes[1].set_ylim([0,0.07])
axes[0].set_ylim([0,0.07])
fig.suptitle('Exposure elasticity for the consumption growth', fontsize=30)
fig.tight_layout()
plt.show()
2.2 Calculate Price Elasticity for Consumption Growth#
Similarly, to calculate the price elasticity for consumption growth using the price_elasticity defined above, we need to input an approximation for the log stochastic discount factor. In the simple case that you will encounter in your problem set, you will be able to deduce this from the consumption growth equation. For now we will presume that we already have the approximation ready:
log_SDF = LinQuadVar({'c' : np.array([[-0.02005034]]),
'x' : np.array([[-0.0299976, -0.02903654]]),
'xw': np.array([[ 0. , 0.00001026, 0. , -0.03199734, -0.12719014, 0. ]]),
'xx': np.array([[ 0.0000006 , 0. , 0.0000006 , -0.00725869]]),
'w' : np.array([[-0.06399468, -0.24439539, 0.06087257]])}
,shape=(1,n_X,n_W))
Next, we compute price elasticities for the three shocks using the function price_elasticity:
quantile = [0.1, 0.5, 0.9]
price_elas_shock_0 = [price_elasticity(gc_tp1, log_SDF, X1_tp1, X2_tp1, T, shock=0, percentile=p) for p in quantile]
price_elas_shock_1 = [price_elasticity(gc_tp1, log_SDF, X1_tp1, X2_tp1, T, shock=1, percentile=p) for p in quantile]
price_elas_shock_2 = [price_elasticity(gc_tp1, log_SDF, X1_tp1, X2_tp1, T, shock=2, percentile=p) for p in quantile]
We can then plot our results:
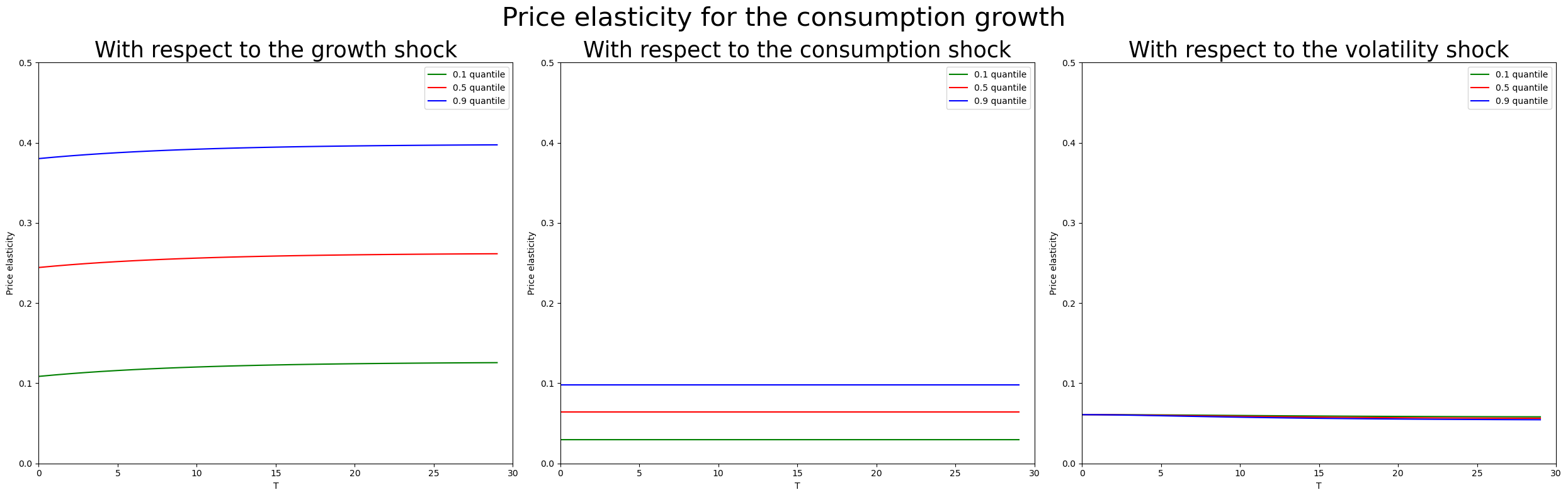
## Plot the price elasticity for consumption growth for only ρ = 2/3 (rho 006)
fig, axes = plt.subplots(1, 3, figsize=(25, 8)) # 1 row, 3 columns for each shock
# Create DataFrames for each shock type with quantiles at ρ = 2/3
price_elas_shock_0_df = pd.DataFrame({
'T': np.arange(T),
'0.1 quantile': price_elas_shock_0[0].flatten(),
'0.5 quantile': price_elas_shock_0[1].flatten(),
'0.9 quantile': price_elas_shock_0[2].flatten()
})
price_elas_shock_1_df = pd.DataFrame({
'T': np.arange(T),
'0.1 quantile': price_elas_shock_1[0].flatten(),
'0.5 quantile': price_elas_shock_1[1].flatten(),
'0.9 quantile': price_elas_shock_1[2].flatten()
})
price_elas_shock_2_df = pd.DataFrame({
'T': np.arange(T),
'0.1 quantile': -price_elas_shock_2[0].flatten(),
'0.5 quantile': -price_elas_shock_2[1].flatten(),
'0.9 quantile': -price_elas_shock_2[2].flatten()
})
# List of data and names for each shock
plot_elas = [price_elas_shock_1_df, price_elas_shock_0_df,price_elas_shock_2_df]
shock_name = ['growth shock', 'consumption shock', 'volatility shock']
quantiles = ['0.1 quantile', '0.5 quantile', '0.9 quantile']
colors = ['green', 'red', 'blue']
# Loop over each shock to plot on its respective axis
for k, ax in enumerate(axes):
for qtl, color in zip(quantiles, colors):
sns.lineplot(data=plot_elas[k], x='T', y=qtl, ax=ax, color=color, label=qtl)
ax.set_xlabel('T')
ax.set_ylabel('Price elasticity')
ax.set_title(f'With respect to the {shock_name[k]}', fontsize=25)
axes[0].set_ylim([0,0.5])
axes[1].set_ylim([0,0.5])
axes[2].set_ylim([0,0.5])
axes[0].set_xlim([0,30])
axes[1].set_xlim([0,30])
axes[2].set_xlim([0,30])
fig.suptitle('Price elasticity for the consumption growth', fontsize=30)
fig.tight_layout()
plt.show()
2.3 Additional Features#
In general, you will not have to input the approximations of the state and consumption growth variables manually. Instead, these will be the outputs of our solution code. We have included some sample solutions of the long-run risk model with different parameters of \(\rho\) below.
import pickle
pd.options.display.float_format = '{:.3g}'.format
sns.set(font_scale = 1.5)
"""
load the long-run risk model solutions when ρ = 2/3, 1, 1.5, 10
"""
with open(workdir + '/data/res_006.pkl', 'rb') as f:
res_006 = pickle.load(f)
with open(workdir + '/data/res_010.pkl', 'rb') as f:
res_010 = pickle.load(f)
with open(workdir + '/data/res_015.pkl', 'rb') as f:
res_015 = pickle.load(f)
with open(workdir + '/data/res_100.pkl', 'rb') as f:
res_100 = pickle.load(f)
Then we can access the approximations without inputting them manually, for example:
Below is a brief UI to select parameters shown in the long-run risk model. The stochastic volatility process has been normalized with its mean equal to 1. By changing the inputs of parameters, we can see how shock elasticities vary with respect to these parameters.
from ipywidgets import interact
from BY_example_sol import solve_BY_elas
interact(solve_BY_elas, γ=[('5',5), ('10',10),('15',15),('20',20)],\
β=[('0.995',0.995),('0.998',0.998), ('0.999',0.999)],\
ρ=[('2/3', 2./3),('1', 1.0001),('1.5', 1.5),('10', 10)],\
α=[('0.969',0.969),('0.979',0.979),('0.989',0.989)],\
ϕ_e=[('0.0002',0.0002),('0.0003432',0.0003432),('0.0004',0.0004)],\
ν_1=[('0.977',0.977),('0.987',0.987),('0.997',0.997)],\
σ_w=[('0.03',0.03),('0.0378',0.0378),('0.04',0.04)],\
μ=[('0.0005', 0.0005),('0.0015', 0.0015),('0.003',0.003)],\
ϕ_c=[('0.002',0.002),('0.0078',0.0078),('0.01',0.01)]);
3. Shock Elasticity Appendix#
3.1 Analytical framework#
Shock elasticities are used to quantify the date \(t\) impact on values of exposure to the shock \( (\alpha_0 + \alpha_1 X_0) \cdot W_1\) at date one. It has the form shown in equation 3:
Using the linear-quadratic dynamics of section 1, the computer software recursively computes the logarithm of the denominator of formula (3):
Form
Conveniently, we can express the outcomes as:
for some specification of \({\widetilde \Phi}_i\), \(i=0,1,2,3\). In words, the \({\mathbb M}\) operator maps linear-quadratic functions into linear-quadratic functions. The code uses this mapping repeatedly.
By a direct application of the Law of Iterated Expectations we have that
where \({\mathbb M}^{t-1}[1]\) means to apply the operator \({\mathbb M}\) \(t-1\) times in succession to a function that is identically one. Observe that \({\mathbb M}^{t-1}[1]\) is a function of \(x\).
The function _Φ_star defined below calculates the linear-quadratic dynamic coefficients in \(\mathbb{M}\) mappings and iterations.
To complete the calculation of the elasticity, note that
This leads us to construct the nonegative random variable:
Notice that \(L_{t}\) depends only date one information and has expectation one conditioned on date zero information. Multiplying this positive random variable by \(W_1\) and taking expectations is equivalent to changing the conditional probability distribution and evaluating the conditional expectation of \(W_1\) under this change of measure. Since \(W_1\) is normally distributed, the exponential quadratic construction of \(L_{t}\) implies that \(W_1\) remains normally distributed but with a different mean and covariance matrix. The computer codes use this observation to evaluate formula (5) by taking an altered conditional expectation of \(W_1\).
For the purposes of the code, denote the conditional mean induced by \(L_{t}\) as \(\mu_{t}^0 + \mu_{t}^1 x_1\) and the conditional covariance matrix \({\widetilde \Sigma}_t\).
def _Φ_star(log_M_growth, X1_tp1, X2_tp1, T):
r"""
Computes :math:`\Phi^*_{0,t-1}`, :math:`\Phi^*_{1,t-1}`, :math:`\Phi^*_{2,t-1}`, :math:`\Phi^*_{3,t-1}` in equation (4).
Parameters
----------
log_M_growth : LinQuadVar
Log growth of multiplicative functional M.
e.g. log consumption growth, :math:`\log \frac{C_{t+1}}{C_t}`
X1_tp1 : LinQuadVar
Stores the coefficients of laws of motion for X1.
X2_tp2 : LinQuadVar or None
Stores the coefficients of laws of motion for X2.
T : int
Time horizon.
Returns
-------
Φ_star_1tm1_all : (T, 1, n_X) ndarray
Φ_star_2tm1_all : (T, 1, n_X) ndarray
Φ_star_3tm1_all : (T, 1, n_X**2) ndarray
"""
_, n_X, _ = X1_tp1.shape
Φ_star_1tm1_all = np.zeros((T, 1, n_X))
Φ_star_2tm1_all = np.zeros((T, 1, n_X))
Φ_star_3tm1_all = np.zeros((T, 1, n_X**2))
log_M_growth_distort = log_E_exp(log_M_growth)
X1X1 = kron_prod(X1_tp1, X1_tp1)
for i in range(1, T):
Φ_star_1tm1_all[i] = log_M_growth_distort['x']
Φ_star_2tm1_all[i] = log_M_growth_distort['x2']
Φ_star_3tm1_all[i] = log_M_growth_distort['xx']
temp = next_period(log_M_growth_distort, X1_tp1, X2_tp1, X1X1)
log_M_growth_distort = log_E_exp(log_M_growth + temp)
return Φ_star_1tm1_all, Φ_star_2tm1_all, Φ_star_3tm1_all
The function _elasticity_coeff defined below calculates the conditional mean induced by \(L_{t}\) as \(\mu_{0,t} + \mu_{1,t} x_1\) and the covariance matrix as \({\widetilde \Sigma}_{t}.\)
def _elasticity_coeff(log_M_growth, X1_tp1, X2_tp1, T):
r"""
Computes :math:`\mu_{t,0}`, :math:`\mu_{t,1}`, :math:`\tilde{\Sigma}_t`. Corresponding formulas can be found in [3], Jaroslav and Hansen (2014), Appendix B.
Parameters
----------
log_M_growth : LinQuadVar
Log difference of multiplicative functional.
e.g. log consumption growth, :math:`\log \frac{C_{t+1}}{C_t}`
X1_tp1 : LinQuadVar
Stores the coefficients of laws of motion for X1.
X2_tp2 : LinQuadVar or None
Stores the coefficients of laws of motion for X2.
T : int
Time horizon.
Returns
-------
Σ_tilde_t_all : (T, n_W, n_W) ndarray
μ_t0_all : (T, n_W, 1) ndarray
μ_t1_all : (T, n_W, n_X) ndarray
"""
_, n_X, n_W = log_M_growth.shape
Φ_star_1tm1_all, Φ_star_2tm1_all, Φ_star_3tm1_all = _Φ_star(log_M_growth, X1_tp1, X2_tp1, T)
Ψ_0 = log_M_growth['w']
Ψ_1 = log_M_growth['xw']
Ψ_2 = log_M_growth['ww']
Λ_10 = X1_tp1['w']
if log_M_growth.second_order:
Λ_20 = X2_tp1['w']
Λ_21 = X2_tp1['xw']
Λ_22 = X2_tp1['ww']
else:
Λ_20 = np.zeros((n_X,n_W))
Λ_21 = np.zeros((n_X,n_X*n_W))
Λ_22 = np.zeros((n_X,n_W**2))
Θ_10 = X1_tp1['c']
Θ_11 = X1_tp1['x']
Σ_tilde_t_all, μ_t0_all, μ_t1_all \
= _elasticity_coeff_inner_loop(Φ_star_1tm1_all, Φ_star_2tm1_all, Φ_star_3tm1_all, Ψ_0, Ψ_1, Ψ_2, Λ_10, Λ_20, Λ_21, Λ_22, Θ_10, Θ_11, n_X, n_W, T)
return Σ_tilde_t_all, μ_t0_all, μ_t1_all
@njit
def _elasticity_coeff_inner_loop(Φ_star_1tm1_all, Φ_star_2tm1_all, Φ_star_3tm1_all, Ψ_0, Ψ_1, Ψ_2, Λ_10, Λ_20, Λ_21, Λ_22, Θ_10, Θ_11, n_X, n_W, T):
Σ_tilde_t_all = np.zeros((T, n_W, n_W))
μ_t0_all = np.zeros((T, n_W, 1))
μ_t1_all = np.zeros((T, n_W, n_X))
kron_Λ_10_Λ_10 = np.kron(Λ_10,Λ_10)
kron_Θ_10_Λ_10_sum = np.kron(Θ_10,Λ_10) + np.kron(Λ_10,Θ_10)
temp = np.kron(Λ_10, Θ_11[:, 0:1].copy())
for j in range(1, n_X):
temp = np.hstack((temp, np.kron(Λ_10, Θ_11[:, j:j+1].copy())))
kron_Θ_11_Λ_10_term = np.kron(Θ_11, Λ_10) + temp
for t in prange(T):
Φ_star_1tm1 = Φ_star_1tm1_all[t]
Φ_star_2tm1 = Φ_star_2tm1_all[t]
Φ_star_3tm1 = Φ_star_3tm1_all[t]
Σ_tilde_t_inv = np.eye(n_W)- 2 * sym(mat(Ψ_2 + Φ_star_2tm1@Λ_22 + Φ_star_3tm1@kron_Λ_10_Λ_10, (n_W, n_W)))
μ_t0 = (Ψ_0 + Φ_star_1tm1@Λ_10 + Φ_star_2tm1@Λ_20 + Φ_star_3tm1 @ kron_Θ_10_Λ_10_sum).T
μ_t1 = mat(Ψ_1 + Φ_star_2tm1 @ Λ_21 + Φ_star_3tm1 @ kron_Θ_11_Λ_10_term,(n_W, n_X))
Σ_tilde_t_all[t] = np.linalg.inv(Σ_tilde_t_inv)
μ_t0_all[t] = μ_t0
μ_t1_all[t] = μ_t1
return Σ_tilde_t_all, μ_t0_all, μ_t1_all
3.2 Exposure and Price Elasticities#
Then we use the functions above to compute our shock elasticities. Since the shock elasticity function depends on \(x_1\), the code computes percentiles of the shock elasticity based on the stationary distribution of \(x_1\). This is done by the internal function _compute_percentile in exposure_elasticity and price_elasticity.
def exposure_elasticity(log_M_growth, X1_tp1, X2_tp1, T=400, shock=0, percentile=0.5):
r"""
Computes exposure elasticity for M.
Parameters
----------
log_M_growth : LinQuadVar
Log growth of multiplicative functional M.
e.g. log consumption growth, :math:`\log \frac{C_{t+1}}{C_t}`
X1_tp1 : LinQuadVar
Stores the coefficients of laws of motion for X1.
X2_tp1 : LinQuadVar
Stores the coefficients of laws of motion for X2.
T : int
Time horizon.
shock : int
Position of the initial shock, starting from 0.
percentile : float
Specifies the percentile of the elasticities.
Returns
-------
elasticities : (T, n_Y) ndarray
Exposure elasticities.
Reference
---------
Borovicka, Hansen (2014). See http://larspeterhansen.org/.
"""
n_Y, n_X, n_W = log_M_growth.shape
if n_Y != 1:
raise ValueError("The dimension of input should be 1.")
α = np.zeros(n_W)
α[shock] = 1
p = norm.ppf(percentile)
Σ_tilde_t, μ_t0, μ_t1 = _elasticity_coeff(log_M_growth, X1_tp1, X2_tp1, T)
kron_product = np.kron(X1_tp1['x'], X1_tp1['x'])
x_mean = np.linalg.solve(np.eye(n_X)-X1_tp1['x'],X1_tp1['c'])
x_cov = mat(np.linalg.solve(np.eye(n_X**2)-kron_product,
vec(X1_tp1['w']@X1_tp1['w'].T)), (n_X, n_X))
elasticities = _exposure_elasticity_loop(T, n_Y, α, Σ_tilde_t, μ_t0,
μ_t1, percentile, x_mean, x_cov, p)
return elasticities
@njit(parallel=True)
def _exposure_elasticity_loop(T, n_Y, α, Σ_tilde_t, μ_t0, μ_t1, percentile, x_mean, x_cov, p):
elasticities = np.zeros((T, n_Y))
if percentile == 0.5:
for t in prange(T):
elasticity = (α@Σ_tilde_t[t]@μ_t0[t])[0] +(α@Σ_tilde_t[t]@μ_t1[t]@x_mean)[0]
elasticities[t] = elasticity
else:
for t in prange(T):
elasticity = (α@Σ_tilde_t[t]@μ_t0[t])[0] +(α@Σ_tilde_t[t]@μ_t1[t]@x_mean)[0]
A = α@Σ_tilde_t[t]@μ_t1[t]
elasticity = _compute_percentile(A, elasticity, x_cov, p)
elasticities[t] = elasticity
return elasticities
def price_elasticity(log_G_growth, log_S_growth, X1_tp1, X2_tp1, T=400, shock=0, percentile=0.5):
r"""
Computes price elasticity.
Parameters
----------
log_G_growth : LinQuadVar
Log growth of multiplicative functional G.
e.g. log consumption growth, :math:`\log \frac{C_{t+1}}{C_t}`
log_S_growth : LinQuadVar
Log growth of multiplicative functional S.
e.g. log stochastic discount factor, :math:`\log \frac{S_{t+1}}{S_t}`
X1_tp1 : LinQuadVar
Stores the coefficients of laws of motion for X1.
X2_tp2 : LinQuadVar or None
Stores the coefficients of laws of motion for X2.
T : int
Time horizon.
shock : int
Position of the initial shock, starting from 0.
percentile : float
Specifies the percentile of the elasticities.
Returns
-------
elasticities : (T, dim) ndarray
Price elasticities.
Reference
---------
Borovicka, Hansen (2014). See http://larspeterhansen.org/.
"""
if log_G_growth.shape != log_S_growth.shape:
raise ValueError("The dimensions of G and S do not match.")
else:
n_Y, n_X, n_W = log_G_growth.shape
if n_Y != 1:
raise ValueError("The dimension of inputs should be (1, n_X, n_W)")
α = np.zeros(n_W)
α[shock] = 1
p = norm.ppf(percentile)
Σ_tilde_expo_t, μ_expo_t0, μ_expo_t1 \
= _elasticity_coeff(log_G_growth, X1_tp1, X2_tp1, T)
Σ_tilde_value_t, μ_value_t0, μ_value_t1\
= _elasticity_coeff(log_G_growth+log_S_growth, X1_tp1, X2_tp1, T)
kron_product = np.kron(X1_tp1['x'], X1_tp1['x'])
x_mean = np.linalg.solve(np.eye(n_X)-X1_tp1['x'],X1_tp1['c'])
x_cov = mat(np.linalg.solve(np.eye(n_X**2)-kron_product,
vec(X1_tp1['w']@X1_tp1['w'].T)), (n_X, n_X))
elasticities = _price_elasticity_loop(T, n_Y, α, Σ_tilde_expo_t, Σ_tilde_value_t,
μ_expo_t0, μ_value_t0, μ_expo_t1, μ_value_t1,
percentile, x_mean, x_cov, p)
return elasticities
@njit(parallel=True)
def _price_elasticity_loop(T, n_Y, α, Σ_tilde_expo_t, Σ_tilde_value_t,
μ_expo_t0, μ_value_t0, μ_expo_t1, μ_value_t1,
percentile, x_mean, x_cov, p):
elasticities = np.zeros((T, n_Y))
if percentile == 0.5:
for t in prange(T):
elasticity = (α @ (Σ_tilde_expo_t[t] @ μ_expo_t0[t] \
- Σ_tilde_value_t[t] @ μ_value_t0[t]))[0]\
+(α@(Σ_tilde_expo_t[t]@μ_expo_t1[t]@x_mean\
- Σ_tilde_value_t[t] @ μ_value_t1[t]@x_mean))[0]
elasticities[t] = elasticity
else:
for t in prange(T):
elasticity = (α @ (Σ_tilde_expo_t[t] @ μ_expo_t0[t]\
- Σ_tilde_value_t[t] @ μ_value_t0[t]))[0]\
+(α@(Σ_tilde_expo_t[t]@μ_expo_t1[t]@x_mean\
- Σ_tilde_value_t[t] @ μ_value_t1[t]@x_mean))[0]
A = α @ (Σ_tilde_expo_t[t]@μ_expo_t1[t]\
- Σ_tilde_value_t[t]@μ_value_t1[t])
elasticity = _compute_percentile(A, elasticity, x_cov, p)
elasticities[t] = elasticity
return elasticities
@njit
def _compute_percentile(A, Ax_mean, x_cov, p):
r"""
Compute percentile of the scalar Ax, where A is vector coefficient and x follows multivariate normal distribution.
Parameters
----------
A : (N, ) ndarray
Coefficient of Ax.
Ax_mean : float
Mean of Ax.
x_cov : (N, N) ndarray
Covariance matrix of x.
p : float
Percentile of a standard normal distribution.
Returns
-------
res : float
Percentile of Ax.
"""
Ax_var = A@x_cov@A.T
Ax_std = np.sqrt(Ax_var)
res = Ax_mean + Ax_std * p
return res
3.3 Limiting Behavior#
The operator \({\mathbb M}\) typically has a solution to the following equation:
The solution of interest when, it exists, can be deduced by iterating on the \({\mathbb M}\) operator allowing for a constant shift \(\eta^e\). This solution gives a characterization of the limiting elasticity. Construct
The elasticities are given by conditional linear combinations of conditional expectations of \(W_1\) under this limiting change of measure.
To express the equation of interest differently, consider the operator, \({\mathbb P}\) that maps \(\Phi_{0} +\Phi_1 x_1+\Phi_2 x_2 + {\frac 1 2} (x_1)'\Phi_3 x_1\) into \(\exp\left({\mathbb M} \left[ \Phi_{0} +\Phi_1^e x_1+\Phi_2 x_2 + {\frac 1 2} (x_1)'\Phi_3 x_1\right] \right)\). Rewrite equation (6) as:
which is an eigenvalue equation where \(\exp\left[ \Phi_1^e x_1+\Phi_2^e x_2 + {\frac 1 2} (x_1)'\Phi_3^e x_1\right]\) is a postive eigenfunction and \(\exp(\eta)\) is a positive eigenvalue. [1]
The codes below solve the eigenvalue problem using the M_mapping.
def M_mapping(log_M_growth, f, X1_tp1, X2_tp1, second_order = True):
r'''
Computes coefficients of a LinQuadVar after one iteration of M mapping
Parameters
----------
log_M_growth : LinQuadVar
Log difference of multiplicative functional.
e.g. log consumption growth, :math:`\log \frac{C_{t+1}}{C_t}`
f : LinQuadVar
The function M Mapping operate on.
e.g. A function that is identically one, log_f = LinQuadVar({'c': np.zeros((1,1))}, log_M_growth.shape)
X1_tp1 : LinQuadVar
Stores the coefficients of laws of motion for X1.
X2_tp2 : LinQuadVar or None
Stores the coefficients of laws of motion for X2.
second_order: boolean
Whether the second order expansion of the state evoluton equation has been input
Returns
-------
LinQuadVar, stores the coefficients of the new LinQuadVar after one iteration of M Mapping
'''
if second_order:
return log_E_exp(log_M_growth + next_period(f, X1_tp1, X2_tp1))
else:
if X2_tp1 != None:
print('The second order expansion for law of motion is not used in the first order expansion.')
return log_E_exp(log_M_growth + next_period(f, X1_tp1))
def Q_mapping(log_M_growth, f, X1_tp1, X2_tp1, tol = 1e-10, max_iter = 10000, second_order = True):
r'''
Computes limiting coefficients of a LinQuadVar by recursively applying the M mapping operator till convergence, returns the eigenvalue and eigenvector.
Parameters
----------
log_M_growth : LinQuadVar
Log difference of multiplicative functional.
e.g. log consumption growth, :math:`\log \frac{C_{t+1}}{C_t}`
f : LinQuadVar
The function M Mapping operate on.
e.g. A function that is identically one, log_f = LinQuadVar({'c': np.zeros((1,1))}, log_M_growth.shape)
X1_tp1 : LinQuadVar
Stores the coefficients of laws of motion for X1.
X2_tp2 : LinQuadVar or None
Stores the coefficients of laws of motion for X2.
tol: float
tolerance for convergence
max_iter: int
maximum iteration
second_order: boolean
Whether the second order expansion of the state evoluton equation has been input
Returns
-------
Qf_components_log : List of LinQuadVar
stores the coefficients of the LinQuadVar in each iteration of M Mapping
f: LinQuadVar
The function M Mapping operate on.
e.g. A function that is identically one, log_f = LinQuadVar({'c': np.zeros((1,1))}, log_M_growth.shape)
η: float
The eigenvalue
η_series: list of float
The convergence path of the eigenvalue
'''
η_series = []
Qf_components_log = []
for i in range(max_iter):
Qf_components_log.append(f)
if second_order:
f_next = M_mapping(log_M_growth, f, X1_tp1, X2_tp1, second_order = second_order)
else:
if X2_tp1 != None:
print('The second order expansion for law of motion is not used in the first order expansion.')
f_next = M_mapping(log_M_growth, f, X1_tp1, second_order = second_order)
η = (f_next['c'] - f['c']).item()
η_series.append(η)
if distance(f, f_next, ['x', 'xx', 'x2']) < tol:
break
f = f_next
if i >= max_iter-1:
print("Warning: Q iteration may not have converged.")
Qf_components_log.append(f_next)
return Qf_components_log, f, η, η_series
For example, to compute the limiting behaviour of the example above, we can use:
## Calculate exposure elasticity for consumption growth at the limit
log_f = LinQuadVar({'c': np.zeros((1,1))},gc_tp1.shape)
Qf_components_log_C, _, η_C, η_C_series = Q_mapping(gc_tp1, log_f, X1_tp1, X2_tp1, tol = 1e-7)
expo_elas_shock_0_015_limit = [exposure_elasticity(gc_tp1, X1_tp1, X2_tp1, len(η_C_series), shock=0, percentile=p)[-1].item() for p in quantile]
expo_elas_shock_1_015_limit = [exposure_elasticity(gc_tp1, X1_tp1, X2_tp1, len(η_C_series), shock=1, percentile=p)[-1].item() for p in quantile]
expo_elas_shock_2_015_limit = [exposure_elasticity(gc_tp1, X1_tp1, X2_tp1, len(η_C_series), shock=2, percentile=p)[-1].item() for p in quantile]
expo_limit = pd.DataFrame([expo_elas_shock_0_015_limit, expo_elas_shock_2_015_limit,expo_elas_shock_1_015_limit],\
columns = ['0.1 quantile','0.5 quantile','0.9 quantile'],\
index = ['Growth Shock','Consumption Shock','Volatility Shock']).T
expo_limit
| Growth Shock | Consumption Shock | Volatility Shock | |
|---|---|---|---|
| 0.1 quantile | 0.004241 | 0.001273 | 0.019480 |
| 0.5 quantile | 0.008000 | 0.001613 | 0.036833 |
| 0.9 quantile | 0.011759 | 0.001953 | 0.054186 |
