11. Representing and Decomposing Marginal Valuations

Download PDF here Authors: Lars Peter Hansen and Thomas J. Sargent

Date: August 2025 \(\newcommand{\eqdef}{\stackrel{\text{def}}{=}}\)

11.1. Introduction

Partial derivatives of value functions appear in first-order conditions of Markov decision problems and measure marginal valuations. Since controls depend on partial derivatives of value functions, they also feature prominently in max-min formulations of robust control problems. They are also revealing as measures of losses from suboptimal choices and directions of improvements, They are pertinent for both individual decision problems and social evaluations. Marginal valuations are prominent in both public and environmental economics. Robust control theories have been used by [Hansen et al., 1999] to assess impacts of uncertainty on investment and equilibrium prices and quantities, by [Alvarez and Jermann, 2004] to evaluate the welfare consequences of uncertainty, extending [Lucas, 1987]. There is an extensive literature measuring the social cost of carbon with different approaches. See for instance, [Cai et al., 2017], [Nordhaus, 2017], and [Rennert et al., 2022], and [Barnett et al., 2020][1].

This chapter imports insights about stochastic nonlinear impulse response functions that come from asset pricing methods for valuing uncertain cash flows. We apply a formalization derived in [Hansen and Souganidis, 2025]. Our analysis relies on decompositions of partial derivatives that allow researchers to partition quantitative findings into contributing forces. This approach contributes to a broader agenda that aims to improve uncertainty quantification methods. Dynamic stochastic equilibrium models often involve several moving parts. Decomposing sources of implications from such models “opens black boxes” and helps provide plausible explanations of model outcomes. Our asset-pricing perspective allows us to think in terms of state-dependent discounting and stochastic flows reminiscent of stochastic payoffs to be valued. Moreover, this perspective allows us to relate stochastic flow to forcing functions that drive outcomes a dynamic stochastic equilibrium model.

11.2. Discrete time

We start with Markov process

(11.1)\[\begin{split}X_{t+1} = \psi(X_t, W_{t+1}) \\ Y_{t+1} - Y_t = \kappa(X_t, W_{t+1}),\end{split}\]

with \(n\) components of \(X,\) \(Y\) a scalar, and \(W\) is \(k\) dimensional. We also want to study the associated variational processes

(11.2)\[\begin{split}\Lambda_{t+1} = \frac {\partial \psi}{\partial x'} (X_t, W_{t+1}) \Lambda_t \\ \Delta_{t+1} - \Delta_t = \frac {\partial \kappa}{\partial x}(X_t, W_{t+1}) \cdot \Lambda_t .\end{split}\]

We use stochastic impulse responses to provide an “asset pricing” representation of partial derivatives of a value function with respect to one of the components of \(X_0\). Consider a value function that satisfies:

(11.3)\[\begin{split}\begin{align} V(X_t) + Y_t = & \exp(-\delta) \mathbb{E} \left[ V(X_{t+1}) + Y_{t+1} \mid X_t \right] \\ & + [1 - \exp(-\delta)] \left[ U(X_t) + Y_t \right]. \end{align}\end{split}\]

The additive contribution in \(Y_t\) is present in part because of our presumption that the dynamical economic system evolves along a balanced-growth path. We capture the stochastic growth by the \(Y\) dynamics where the state vector process \(X\) is appropriately scaled to induce (asymptotically) stationary dynamics. In particular, suppose that there is a single consumption good \(C_t\) that can be represented as:

(11.4)\[\log C_t = \phi(X_t) + Y_t.\]

We also impose a unitary elasticity of substitution by letting this same expression be the current-period contribution to utility. In this case \(U\) and \(\phi\) agree. Later we discuss relaxations of this simplifying assumption on preferences. The state dynamics and resulting value function might measure outcomes from using some arbitrary collection of decision rules, not necessarily socially optimal ones. To do a local policy analysis, we’ll want to compute marginal valuations for such a value function.

Differentiate both sides of this (11.3) with respect to \(X_t\) and \(Y_t\) and form dot products with appropriate variational counterparts:

(11.5)\[\begin{split}\begin{align} \frac{\partial V}{\partial x}(X_t) \cdot \Lambda_t + \Delta_t = & \exp(-\delta) \mathbb{E}\left[ \frac{\partial V}{\partial x}(X_{t+1}) \cdot \Lambda_{t+1} + \Delta_{t+1} \mid X_t, \Lambda_t, \Delta_t \right] \\ & + [1 - \exp(-\delta)]\left[\frac{\partial U}{\partial x}(X_t) \cdot \Lambda_t + \Delta_t \right] \end{align} \end{split}\]

View equation (11.5) as a stochastic difference equation and solve it forward for \(\frac{\partial V}{\partial x}(X_t) \cdot \Lambda_t + \Delta_t:\)

(11.6)\[\begin{align*} & \frac{\partial V}{\partial x}(X_t) \cdot \Lambda_t + \Delta_t = \cr & [1 - \exp(-\delta)]\sum_{\tau = 0}^\infty \mathbb{E}\left( \exp(-\tau \delta) \left[\frac{\partial U}{\partial x}(X_{t+\tau}) \cdot \Lambda_{t+\tau} + \Delta_{t + \tau}\right] \mid X_t, \Lambda_t, \Delta_t \right) \end{align*}\]

Initialize \(\Lambda_0 = \mathrm{e}_i,\) where \(\mathrm{e}_i\) is a coordinate vector with a one in position \(i\) and \(\Delta_0 = 0.\) This lets us represent the partial derivative of the value function as:

(11.7)\[\begin{align} & \frac{\partial V}{\partial x_i}(x) = \cr & [1 - \exp(-\delta)]\sum_{t = 0}^\infty \exp(-t \delta) \mathbb{E}\left[ \frac{\partial U}{\partial x}(X_{t}) \cdot \Lambda_{t} + \Delta_t \mid X_0 = x, \Lambda_0 = \mathrm{e}_i, \Delta_0 = 0 \right] . \end{align} \]

To obtain an ``asset pricing’’ formula, observe that the marginal utility of consumption is the reciprocal of consumption and write:

\[\frac{\partial U}{\partial x} (X_t) \cdot \Lambda_t + \Delta_t = \left(\frac 1 {C_t}\right) {\exp\left[ \phi(X_t) + Y_t\right]}\left[ \frac {\partial \phi} {\partial x}(X_t) \cdot \Lambda_t + \Delta_t \right]\]

where we use the logarithmic utility function and formula (11.4). The first term on the right side of the equality is the marginal utility of consumption at date \(t\), and the second two terms collective capture the stochastic response for consumption over horizon \(t\). Thus formula (11.7) once we divide \(\frac{\partial V}{\partial x_i}(x)\) by consumption in the initial period to convert the marginal valuation into units of date zero consumption and view

\[\delta {\exp\left[ \phi(X_t) + Y_t\right]}\left[ \frac {\partial \phi} {\partial x}(X_t) \cdot \Lambda_t + \Delta_t \right]\]

as a stochastic flow process.

Remark 11.1

Sometimes it is convenient to apply summation by parts:

\[\begin{split}\begin{align*} & [1 - \exp(-\delta)]\sum_{\tau = 0}^\infty \mathbb{E}\left( \exp(-\tau \delta) \Delta_{t + \tau} \mid X_t, \Lambda_t, \Delta_t \right) \\ & = \sum_{\tau = 1}^\infty \mathbb{E}\left[ \exp(-\tau \delta) \left(\Delta_{t + \tau} - \Delta_{t+\tau -1} \right) \mid X_t, \Lambda_t, \Delta_t \right] + \Delta_t \\ & = \sum_{\tau = 1}^\infty \mathbb{E}\left[ \exp(-\tau \delta) \frac{\partial \kappa}{\partial x}(X_{t+\tau-1}, W_{t+\tau})\cdot \Lambda_{t+ \tau} \mid X_t, \Lambda_t, \right] + \Delta_t . \end{align*}\end{split}\]

Substituting into (11.6) gives:

\[\begin{split}\begin{align} &\frac{\partial V}{\partial x}(X_t) \cdot \Lambda_t + \Delta_t = \cr & [1 - \exp(-\delta)]\sum_{\tau = 0}^\infty \mathbb{E}\left[ \exp(-\tau \delta) \frac{\partial U}{\partial x}(X_{t+\tau}) \cdot \Lambda_{t+\tau} \mid X_t, \Lambda_t, \right] \\ & + \sum_{\tau = 1}^\infty \mathbb{E}\left[ \exp(-\tau \delta) \frac{\partial \kappa}{\partial x}(X_{t+\tau-1}, W_{t+\tau})\cdot \Lambda_{t+ \tau} \mid X_t, \Lambda_t, \right] + \Delta_t. \end{align}\end{split}\]

11.3. Continuous time

A continuous-time formulation allows us to distinguish small shocks (Brownian increments) from large shocks (Poisson jumps). Let’s consider a continuous-time specification with Brown motion shocks, i.e., diffusion dynamics. We can treat jumps as terminal conditions for which we impose continuation values conditioned on a jump taking place. The possibility of a jump contributes to the value function. After developing this approach, we shall extend it to we include valuations that reflect concerns about model misspecifications, i.e., “robust valuations.”

11.3.1. Diffusion dynamics

We start with a Markov diffusion that governs state dynamics

\[\begin{split}\begin{align*} dX_t & = \mu(X_t) dt + \sigma(X_t) dW_t \\ dY_t & = \nu(X_t) dt + \varsigma(X_t) \cdot dW_t. \end{align*}\end{split}\]

that need not be the outcome of an optimization problem.

Using the variational process construction in the previous chapter, recall that

\[d\Lambda_{t}^i = \left(\Lambda_t\right)'\frac{\partial \mu_i}{\partial x}(X_t) dt + \left({\Lambda_t}\right)'\frac{\partial \sigma_i}{\partial x}(X_t) dW_t.\]

With the appropriate stacking, the drift for the composite process \((X,\Lambda)\) is:

(11.8)\[\begin{split}\mu^a(x,\lambda) \overset{\text{def}}{=} \begin{bmatrix} \mu(x) \\ \lambda'{\frac {\partial \mu_i} {\partial x} }(x) \\ ... \\ \lambda'{\frac {\partial \mu_n} {\partial x} }(x) \end{bmatrix},\end{split}\]

and the composite matrix coefficient on \(dW_t\) is given by

(11.9)\[\begin{split}\sigma^a(x,\lambda) \overset{\text{def}}{=} \begin{bmatrix} \sigma(x) \\ \lambda'\frac {\partial \sigma_1 }{\partial x}(x)\\ ... \\ \lambda' \frac {\partial \sigma_n }{\partial x}(x) \end{bmatrix}.\end{split}\]

Similarly, \(\Delta\) is the scalar variational process associated with \(Y\) with evolution

\[d \Delta_t = \Lambda_t \cdot \frac {\partial \nu}{\partial x} (X_t)dt + {\Lambda_t}' \frac {\partial \varsigma}{\partial x'} dW_t \]

11.3.2. An initial representation of a partial derivative

Consider the evaluation of discounted utility where the instantaneous contribution is \(U(x)\) where \(x\) is the realization of a state vector \(X_t\). The function \(U\) satisfies a Feynman-Kac (FK) equation:

(11.10)\[\begin{align} 0 = & \delta \left[U(x) + y\right] - \delta \left[V(x) + y \right] + \mu(x) \cdot \frac {\partial V}{\partial x}(x) + \nu(x) \cr &+ {\frac 1 2 }{\rm trace}\left[\sigma(x)' \frac {\partial^2 V}{\partial x \partial x'}(x) \sigma(x) \right]. \end{align}\]

As in the discrete-time example, we want to represent

\[V_{x_i}(x) = {\frac {\partial V}{\partial x_i}}(x) \]

as an expected discounted value of a marginal impulse response of future \(X_t\) to a marginal change of the \(i^{th}\) coordinate of \(x.\)

By differentiating Feynman-Kac equation (11.10) with respect to each coordinate, we obtain a vector of equations, one for each state variable. We then form the dot product of this vector system with respect to \(m\) to obtain a scalar equation system that is of particular interest. The resulting equation is a Feynman-Kac equation for the scalar function:

\[\lambda \cdot \frac {\partial V}{\partial x}\]

as established in the Appendix. Given that the equation to be solved involves both \(\lambda\) and \(x\), this equation uses the diffusion dynamics for the joint process \((X,\Lambda)\).

The solution to this Feynman-Kac equation takes the form of a discounted expected value:

(11.11)\[\begin{align} & \frac {\partial V}{\partial x}(X_0) \cdot \Lambda_0 + \Delta_0 \cr &= \delta \int_0^\infty \exp( - \delta t ) {\mathbb E} \left[ \frac {\partial U}{\partial x} (X_{t}) \cdot \Lambda_{t} + \Delta_t \mid X_0, \Lambda_0, \Delta_0 \right] dt. \end{align} \]

By initializing the state vector \(\Lambda_0\) to be a coordinate vector of zeros in all entries except \(i\) and \(\Lambda_0 = 0\), we obtain the formula we want, which gives the partial derivative as a discounted present value using \(\delta\) as the discount rate. The contribution, \(\Lambda_{t},\) is the marginal response of the date \(t\) state vector to marginal change in the \(i^{th}\) component of the state vector at date zero. The marginal change in the date \(t\) state vector induces marginal reward at date \(t\):

\[\delta \left[ \frac {\partial U}{\partial x} (X_{t})\cdot \Lambda_{t} + \Delta_t \right]\]

which provides us with a useful interpretation as an asset price. The process \(\Lambda\) gives a vector counterpart to a stochastic discount factor process and \(\delta \left[\frac {\partial U}{\partial x} (X_{t}) + \Delta_t \right]\) gives the counterpart to a cash flow to be valued.

Decomposition I

One application of representation (11.11) uses the discounted expected impulse response:

\[\delta \exp( - \delta t ) {\mathbb E} \left[ \frac {\partial U}{\partial x} (X_{t}) \cdot \Lambda_{t} \mid X_0, \Lambda_0, \Delta_0 \right]. \]

for \(t \ge 0\) and for \(j=1,2,...,n\) along with

\[\delta \exp( - \delta t ) {\mathbb E} \left[ \Delta_t \mid X_0, \Lambda_0, \Delta_0 \right] \]

for \(t \ge 0\) to form an additive decomposition of the marginal valuation of one of the state variables (as determined by an initialization of \(\Lambda_0.\)) into contributions of each of the future state variables. Write:

\[\frac {\partial U}{\partial x} (X_{t}) \cdot \Lambda_{t} = \sum_{j=1}^n \frac {\partial U}{\partial x_j} (X_{t})\Lambda_{j,t}.\]

Then

\[\begin{align} & \frac {\partial V}{\partial x}(X_0) \cdot \Lambda_0 \cr &= \sum_{j=1}^n \delta \int_0^\infty \exp( - \delta t ) {\mathbb E} \left[ \frac {\partial U}{\partial x_j} (X_{t}) \cdot \Lambda_{j,t} \mid X_0, \Lambda_0, \Delta_0=0 \right] dt. \end{align}\]

for \(j=1,2,..., n\) provides \(n\) different contributions to the marginal valuation. \(\frac {\partial V}{\partial x}(X_0) \cdot \Lambda_0\) contributed by each of the state variables. This decomposition reveals the importance of state variable interactions in the valuation of any of the state variables.

Remark 11.2

Representations similar to (11.9) appear in the sensitivity analyses of options prices. See [Fournie et al., 1999].

11.3.3. Allowing IES to differ from unity

We briefly sketch an extension allowing for an intertemporal elasticity substitution to be different from unity for a recursive utility specification.
Let \(\rho\) be the inverse of the intertemporal elasticity of substitution and consider the utility recursion:

\[\begin{split}& \left(\frac{\delta}{1-\rho}\right)\left(\exp\left[(1-\rho)\left(U(X_t)+Y_t - {V}(X_t)- Y_t\right)\right]-1\right) \\ & + \mu_{v,t} = 0. \end{split}\]

where \({\mu}_{v,t}\) is the local mean of \({V}(X) + Y\) with the robust adjustment discussed previous subsection. Compute:

\[\begin{align} & \frac{\partial}{\partial x} \left(\frac{\delta}{1-\rho}\right) \left( \exp\left[(1-\rho)\left[U(x) - V(x)\right]\right]-1 \right) \cr &= \delta \exp\left[(1-\rho)\left[U(x) - {V}(x)\right]\right] \left[\frac {\partial U} {\partial x} (x) -\frac{\partial{V}}{\partial x}(x)\right]. \end{align} \]

With this calculation, we modify the previous formulas by replacing the subjective discount factor, \(\exp(-\delta t),\) with

\[Dis_t \eqdef \exp\left(-\int_0^t \delta \exp\left[(1-\rho)\left[U\left(X_\tau\right) -V(X_\tau)\right]\right] d\tau \right).\]

Thus the instantaneous discount rate is now state dependent and depends on the both how the current utility compares to the continuation value and on whether \(\rho\) is greater or less than one. When the current utility exceeds the continuation value, the discount rate is scaled up when \(\rho\) exceeds one, and it is scaled down when \(\rho\) is less than one.

We replace the instantaneous contribution to the flow term, \(\delta \frac {\partial U} {\partial x} (X_t),\) with:

\[ \delta\exp\left[(1-\rho)\left[U(X_t)- V(X_t)\right]\right]\frac {\partial U}{\partial x} (X_t)\]

Combining these contributions gives:

\[\begin{split}& \frac {\partial V}{\partial x}\left( X_0 \right) + \Delta_0 = \\ & \delta \widetilde{\mathbb E}\left( \int_0^\infty Dis_t \exp\left[(1-\rho)\left[U\left( X_t \right)- V(X_t)\right]\right] \right. \cr & \hspace{1cm} \left. \times \left(\frac {\partial U} {\partial x} (X_t) \cdot \Lambda_t + \Delta_t \right) dt \mid X_0, \Lambda_0, \Delta_0 \right) .\end{split}\]

For notational simplicity, we will focus in the special case in which \(\rho = 1\) in what follows.

11.3.4. Robustness

We next consider a general class of drift distortions that can help us study model misspecification concerns. We initially explore the consequences of exogenously-specified drift distortions. After that, we show how such a distortion can emerge endogenously as a decision-maker’s response to concerns about model misspecifications.

For diffusions, we entertain modifications to the Brownian increment. Instead of \(W\) being a multivariate Brownian motion, we allow it to have a drift \(H\) under a change in the probability distribution. We index the alternative probability specifications with their corresponding drift processes \(H\). Locally,

\[dW_t = H_t dt + dW^H_t\]

where \(W^H\) is a Brownian motion under the \(H\) probability. Given that both the distribution parameterized by \(H\) and the baseline distribution for the increment are normals with an identity matrix as the local covariance matrix, the local measure of relative entropy is given by the quadratic term:

\[{\frac 1 2} H_t \cdot H_t .\]

See [James, 1992], [Anderson et al., 2003], and [Hansen et al., 2006] for further discussions of this continuous-time formulation. [Cerreia-Vioglio et al., 2025] provide an axiomatic foundation for misspecification aversion.

Again we suppose any decision or policy rules are embedded in the baseline state dynamics. To make a robustness adjustment, we introduce a minimizing or adversarial decision maker who minimizes the discounted expected utility by choice of the drift distortion. Consider a value function, \(V,\) that solves:

(11.12)\[\begin{align} 0 &= \min_h\hspace{.2cm} \delta\left[ U(x) + y\right] - \delta \left[ V(x) + y \right]+ {\frac \xi 2}|h|^2 \cr & + \left[\mu(x) +\sigma(x)h \right] V_x(x) + \nu(x) + \varsigma(x) \cdot h \cr & + {\frac 1 2} {\rm trace} \left[ \sigma (x)' V_{xx}(x) \sigma(x) \right]. \end{align}\]

The minimizing \(h\) in (11.12) expressed as a function of \(x\) satisfies:

(11.13)\[h^*(x) = - \frac 1 \xi \left[ \sigma'(x) V_x(x) + \varsigma(x) \right].\]

We use this solution to provide an alternative perspective on the implications of robustness.
Define the drift distortion:

\[H_t^* \eqdef h^*\left({\overline X}_t \right).\]

We alter the stochastic dynamics for the original state vector to be:

\[d X_t = \mu(X_t)dt + \sigma(X_t) h^* \left( \overline{X}_t \right) dt + \sigma(X_t) dW_t^{H^*}\]

where \(\overline{X}\) satisfies:

\[d \overline{X}_t = {\bar \mu}\left( \overline{X}_t \right) dt + {\bar \sigma} \left({\overline X}_t\right) dW_t^{H^*}\]

and

\[\begin{align*} {\bar \mu}\left( \overline{X}_t \right) \eqdef & \mu\left( {\overline X}_t \right) + {\bar \sigma} \left({\overline X}_t\right) h^*\left( {\overline X}_t\right) \cr {\bar \sigma} \left({\overline X}_t\right) = & \sigma\left( {\overline X}_t\right) \end{align*}\]

for the initialization \({\overline X}_0 = X_0\). Given this initial condition, by design \(X_t = {\overline X}_t\) for \(t \ge 0.\) We use the constructed process \(\{ {\overline X}_t : t \ge 0 \}\) for the sole purpose of representing the minimizing drift distortion.

The value function of interest is now:

(11.14)\[\begin{align} 0 = \hspace{.2cm} & \delta \left[U(x) + y\right] - \delta \left[ {\overline V}(x,{\bar x}) + y \right] + {\frac \xi 2}|h^*(\bar x)|^2 \cr & + {\overline V}_x(x, {\bar x} ) \cdot \left[ \mu(x) +\sigma(x)h^*(\bar x) \right] \cr & + \nu(x) + \varsigma(x ) \cdot h^*(\bar x) + {\overline V}_{\bar x}(x, {\bar x} ) \cdot {\bar \mu}({\bar x}) \cr & + {\frac 1 2} {\rm trace} \begin{bmatrix} \sigma (x)' & {\bar \sigma}({\bar x})' \end{bmatrix} \begin{bmatrix} V_{xx'}(x,{\bar x}) & V_{x{\bar x}'}(x,{\bar x}) \cr V_{{\bar x} x'}(x,{\bar x}') & V_{{\bar x} {\bar x}'}(x,{\bar x}) \end{bmatrix}\begin{bmatrix} \sigma(x) \cr {\bar \sigma}({\bar x}) \end{bmatrix}. \end{align}\]

By design:

\[{\overline V}(x,x) = V(x)\]

for \(V\) that satisfies (11.12). Note that the HJB equation, as posed, allows for \({\bar x} \ne x\). Importantly, there is no contribution from differentiating \(H\) with respect to \(x\) since \(H\) only depends on the \(\bar{X}_t\) process. Confronted with the value function \({\overline V}(x,{\bar x})\), suppose a minimizing decision maker solves: [ \min_{{\bar x}} {\overline V}_{\bar x}(x, {\bar x}). ] Given the original minimization problem, the solution is necessarily: \({\bar x} = x\) implying that

\[{\overline V}_{\bar x}(x,x) = 0. \]

As a consequence:

\[\begin{split}{\overline V}_x(x,x) & = V_x(x) \\ {\overline V}_{xx'}(x,x) + {\overline V}_{x{\bar x}'}(x,x) & = V_{xx'}(x) \end{split}\]

HJB equation (11.12) implies a corresponding Feynman-Kac equation:

\[\begin{align*} 0 &= \hspace{.2cm} \delta\left[ U[x,d^*(x)] + y\right] - \delta \left[ V(x) + y \right]+ {\frac \xi 2}|h^*(x) |^2 \cr & + \left[\mu[x,d^*(x)] +\sigma[x,d^*(x)]h^*(x) \right] V_x(x) + \nu(x) + \varsigma(x) \cdot h*(x) \cr & + {\frac 1 2} {\rm trace} \left( \sigma [x,d^*(x)]' V_{xx}(x) \sigma[x,d^*(x)] \right). \end{align*}\]

Differentiate this equation with respect to \(x\):

\[\begin{split}\begin{align} 0 = & - \delta V_x + \delta U_x + V_{xx}\left(\mu +\sigma h^* \right) + (\mu_x)'V_x + {\rm{mat}} \left\{ \left(\frac {\partial \sigma_i} {\partial x} \right) h^* \right\}'V_x \cr & + \frac{\partial \nu}{\partial x} + \frac {\partial \varsigma'} {\partial x} h^* \\ & + {\frac \partial {\partial x}} \left[{\frac 1 2} {\rm trace} \left( \sigma' V_{xx} \sigma \right) \right] \end{align}\end{split}\]

where \(\rm{mat}\) denotes a matrix formed by stacking the column arguments. This expression uses the first-order conditions for \(h^*\) and an “Envelope Theorem” to cancel some terms. In this way, we can represent the partial derivative vector of the value function as:

\[\begin{align*} & \frac {\partial V}{ \partial x}(X_0) \cdot \Lambda_0 + \Delta_0\cr &= \delta \int_0^\infty \exp(-\delta t) \widetilde{\mathbb{E}} \left( \frac \partial {\partial x} U\left(X_{t}\right) \cdot \Lambda_{t} + \Delta_t \mid X_0, \Lambda_0, \Delta_0 \right). \end{align*}\]

We use the \({\widetilde {\mathbb E}}\) notation because we are using impulse responses computed under the uncertainty adjusted-state evolution implied by imposing \(\{ H_t^* : t \ge 0 \}\). Armed with change of probability measure, we may apply Decomposition I.

Remark 11.3

Robust control theory goes further by exploring ramification for the decision rule itself. The construction that we described for valuation can be extended for the control framework as well. We explore both a recursive representation of a two player game, and we pose the decision problem as a Stackelberg game solved from a date zero perspective. The maximizing decision maker takes as given, a drift distortion process, \(\{H_t : t \ge 0 \},\) when optimizing by choice of a decision process \(\{D_t : t \ge 0\}\) with realizations in \(\mathcal D\). The minimizing decision maker then optimizes by choice \(H\). This solution is posed in the space of stochastic processes.

We analyze this problem following on insights in [Fleming and Souganidis, 1989].

Consider first a recursive formulation in which we find a value function, \(V,\) that solves:

(11.15)\[\begin{align} 0 &= \max_{d \in {\mathcal D} } \min_h \hspace{.2cm} \delta\left[ U(x,d) + y\right] - \delta \left[ V(x) + y \right]+ {\frac \xi 2}|h|^2 \cr & + \left[\mu(x,d) +\sigma(x,d)h \right] V_x(x) + \nu(x) + \varsigma(x,d) \cdot h \cr & + {\frac 1 2} {\rm trace} \left[ \sigma (x,d)' V_{xx}(x) \sigma(x,d) \right]. \end{align}\]

Notice that this value function is constructed by solving a recursive version of the zero-sum game.

One of the conditions that [Fleming and Souganidis, 1989] impose is called the Bellman-Isaacs equation, which requires that exchanging orders of \(\min\) and \(\max\) does not alter the value function for the recursive game. In effect, [Fleming and Souganidis, 1989] show that coupled dynamic programs characterize the two-player, zero-sum game that interests us, as well as some other two-player, zero-sum games. Following [Hansen et al., 2006], this approach gives us the analogous recipe for constructing a minimizing drift distortion process \(\{H_t : t \ge 0\}\) as we used for robust valuation. The minimizing \(h^*\) in (11.15) expressed now as a function of \({\bar x}\) as well as the corresponding maximizing \(d^*\) express in terms of \({\bar x}\) results in \({\overline X}\) dynamics with

\[\begin{align*} {\bar \mu}\left( \overline{X}_t \right) \eqdef & \mu\left[ {\overline X}_t, d^*\left( {\overline X}_t \right) \right] + {\bar \sigma} \left({\overline X}_t\right) h^*\left( {\overline X}_t\right) \cr {\bar \sigma} \left({\overline X}_t\right) \eqdef & \sigma\left[ {\overline X}_t, d^*\left( {\overline X}_t \right) \right] \end{align*}\]

for the initialization \({\overline X}_0 = X_0\). As was true previously, given this initial condition, by design \(X_t = {\overline X}_t\) for \(t \ge 0.\)

The maximizing decision maker takes \(\{ {\overline X}_t : t \ge 0\}\) as exogenous when optimizing. We write the stochastic dynamics for the original state vector as:

\[d X_t = \mu(X_t, D_t)dt + \sigma(X_t, D_t) h^* \left( \overline{X}_t \right) dt + \sigma(X_t, d_t ) dW_t^{H^*}.\]

The HJB equation for the maximizing decision maker (taking the minimizing solution as given) is:

(11.16)\[\begin{align} 0 = \hspace{.2cm} & \max_{d \in {\mathcal D}} \hspace{.2cm} \delta \left[{\overline U}(x,d) + y\right] - \delta \left[ {\overline V}(x,{\bar x}) + y \right] + {\frac \xi 2}|h^*(\bar x)|^2 \cr & + {\overline V}_x(x, {\bar x} ) \cdot \left[\mu(x,d) +\sigma(x,d)h^*(\bar x) \right] \cr & + \nu(x) + \varsigma(x ) \cdot h^*(\bar x) \ + {\overline V}_{\bar x}(x, {\bar x} ) \cdot {\bar \mu}({\bar x}) \cr & + {\frac 1 2} {\rm trace} \begin{bmatrix} \sigma (x,d)' & {\bar \sigma}({\bar x})' \end{bmatrix} \begin{bmatrix} V_{xx'}(x,{\bar x}) & V_{x{\bar x}'}(x,{\bar x}) \cr V_{{\bar x} x'}(x,{\bar x}') & V_{{\bar x} {\bar x}'}(x,{\bar x}) \end{bmatrix}\begin{bmatrix} \sigma(x,d) \cr {\bar \sigma}({\bar x}) \end{bmatrix}. \end{align}\]

Again we find that:

\[\begin{split}{\overline V}_x(x,x) & = V_x(x) \\ {\overline V}_{xx'}(x,x) + {\overline V}_{x{\bar x}'}(x,x) & = V_{xx'}(x). \end{split}\]

Moreover the solution \({\bar d}\) to HJB equation (11.16) satisfies:

\[{\bar d}(x,x) = d^*(x). \]

from the recursive control solution. This findings support again the application of Decomposition I under our computation of an uncertainty adjusted probability measure.

Remark 11.4

While we demonstrated that we can treat a drift distortion as exogenous to the original state dynamics, for some applications we will want to view it as a change in the endogenous dynamics that are reflected (11.13).

11.3.5. Jumps

We study a pre-jump functional equation in which jump serves as a continuation value. We allow multiple types of jumps, each with its own state-dependent intensity. We denote the intensity of a jump of type \(\ell\) by \(\mathcal{J}^\ell(x)\); a corresponding continuation value after a jump of type \(\ell\) has occurred is \(V^\ell(x)+y\). In applications, we’ll compute post-jump continuation value \(V^\ell\), as components of a complete model solution. To simplify the notation, we impose that \(\rho = 1,\) but it is straightforward to incorporate the \(\rho \ne 1\) extension we discussed in the previous subsection.

As in [Anderson et al., 2003], an HJB equation that adds concerns about robustness to misspecifications of jump intensities includes a robust adjustment to the intensities. The minimizing objective and constraints are separable across jumps. Thus we solve:

\[\min_{g^\ell} \mathcal{J}^\ell \left[ g^\ell \left(V^\ell - V)\right) + \xi \left( 1 - g^\ell + g^\ell \log g^\ell \right)\right]\]

for \(\ell = 1,2, ..., L\), where \(g^\ell \ge 0\) alters the intensity of type \(\ell,\) and the term

\[\mathcal{J}^\ell\left[1 - g^\ell + g^{\ell}\log g^\ell\right]\]

measures the relative entropy of jump intensity specifications.

The minimizing \(g^{\ell}\) is

\[g^{\ell*} = \exp \left[ - \frac 1 \xi \left (V^\ell - V\right) \right]\]

with a minimized objective given by

(11.17)\[\begin{align} & \exp \left[ - \frac 1 \xi \left (V^\ell - V\right) \right] \left(V^\ell - V)\right) + \xi - \xi \exp \left[ - \frac 1 \xi \left (V^\ell - V)\right) \right] \cr & - \left(V^\ell - V\right)\exp \left[ - \frac 1 \xi \left (V^\ell - V)\right) \right] \cr & = \xi \left(1- \exp \left[ - \frac 1 \xi \left (V^\ell - V\right) \right]\right) \end{align}.\]

is increasing and concave in the value function difference: \(V^\ell - V\). A gradient inequality for a concave function implies that

\[\xi \left(1- \exp \left[ - \frac 1 \xi \left (V^\ell - V\right) \right]\right) \le V^\ell - V.\]

Remark 11.5

The deduce the formula for relative entropy and jumps, consider a discrete-time approximation whereby the probability of a jump of type \(\ell\) over an interval of time \(\epsilon\) is (approximately ) \(\epsilon{\mathcal J}^\ell g^\ell\) and probability of not jumping \(1 - \epsilon{\mathcal J}^\ell g^\ell\) where \(g^\ell = 1\) at the baseline probability specification. The approximation becomes good when \(\epsilon\) declines to zero. The corresponding (approximate) relative entropy is

\[\begin{aligned} & \left(\log \epsilon + \log {\mathcal J}^\ell + \log g^\ell - \log \epsilon - \log {\mathcal J}^\ell \right) \epsilon {\mathcal J}^\ell g^\ell \cr & + \left[ \log \left( 1 - \epsilon {\mathcal J}^\ell g^\ell \right) - \log \left( 1 - \epsilon {\mathcal J}^\ell \right) \right] \left( 1 - \epsilon g^\ell {\mathcal J}^\ell \right) \end{aligned}\]

Differentiate this expression with respect to \(\epsilon\) to obtain:

\[\log g^\ell {\mathcal J}^\ell g^\ell - {\mathcal J}^\ell g^\ell + {\mathcal J}^\ell = {\mathcal J}^\ell \left( g^\ell \log g^\ell - g^\ell +1\right). \]

In what follows we will also be interested in the partial derivative of the minimized function given in (11.17) with respect to the state vector:

\[g^{\ell*} \left(\frac {\partial V^\ell}{\partial x} - \frac {\partial V}{\partial x} \right)\]

where \(g^{\ell*}\) is the minimizer used to alter the jump intensity.

When constructing the HJB equation, we continue to include the diffusion dynamics and now incorporate the \(L\) possible jumps. The usual term:

\[ \sum_{\ell=1}^L \mathcal{J}^\ell \left (V^\ell - V\right) .\]

is replaced by

\[\xi \sum_{\ell=1}^L \mathcal{J}^\ell \left(1- \exp \left[ - \frac 1 \xi \left (V^\ell - V\right) \right]\right)\]

as an adjustment for robustness in the jump intensities.
The resulting HJB equation is:

\[\begin{split}\begin{align} 0 = \min_{h} & - \delta V + \delta U + {\frac{\xi}{2}}|h|^2 +\left[\mu +\sigma h\right]\cdot \frac {\partial V}{\partial x} + \nu + \varsigma \cdot h\\ & + {\frac{1}{2}}{\rm trace}\left[\sigma'\frac {\partial^2 V }{\partial x \partial x'}\sigma\right] \\ & + \xi \sum_{\ell=1}^L \mathcal{J}^\ell \left(1- \exp \left[ - \frac 1 \xi \left (V^\ell - V\right) \right]\right) \end{align}\end{split}\]

We again construct a Feynman-Kac equation by substituting in \(h^*(x)\). Applying an Envelope Theorem to first-order conditions for minimization tells us that \(h^*(x)\) should not contribute to the derivatives of the value function. This leads us to focus on:

(11.18)\[\begin{split}\begin{align*} 0 = & -\delta \frac {\partial V }{\partial x} + \delta \frac {\partial U }{\partial x} + \frac {\partial^2 V }{\partial x \partial x'}\left(\mu +\sigma h^*\right)\\ & + \left( \frac {\partial \mu'}{\partial x} \right) \frac {\partial V }{\partial x} + {\rm{mat}}\left\{\left(\frac{\partial \sigma_i}{\partial x}\right)h^*\right\}' \frac {\partial V }{\partial x}\\ & +\frac{\partial}{\partial x}\left[\frac{1}{2}{\rm trace}\left(\sigma' \frac {\partial^2 V }{\partial x \partial x'} \sigma\right)\right] \\ & + \xi \sum_{\ell=1}^L\frac {\partial \mathcal{J}^{\ell}}{\partial x} \left(1- \exp \left[ - \frac 1 \xi \left (V^\ell - V\right) \right]\right) \\ & +\sum_{\ell=1}^L\mathcal{J}^{\ell}g^{\ell*} \left(\frac {\partial V^\ell}{\partial x} - \frac {\partial V}{\partial x} \right). \end{align*}\end{split}\]

It is revealing to rewrite equation (11.18) as:

\[\begin{split}\begin{align*} 0 = & -\left(\delta + \sum_{\ell=1}^L\mathcal{J}^{\ell}g^{\ell*}\right)\frac {\partial V }{\partial x} + \delta \frac {\partial U }{\partial x} \\ & + \frac {\partial^2 V }{\partial x \partial x'}\left(\mu +\sigma h^*\right) + \left( \frac {\partial \mu'}{\partial x}\right)'\frac {\partial V }{\partial x} + {\rm{mat}}\left\{\left(\frac{\partial \sigma_i}{\partial x}\right)h^*\right\}'\frac {\partial V }{\partial x} \\ & + \frac{\partial}{\partial x}\left[\frac{1}{2}{\rm trace}\left(\sigma'\frac {\partial^2 V }{\partial x \partial x'}\sigma\right)\right] \\ & + \xi \sum_{\ell=1}^L\frac {\partial \mathcal{J}^{\ell}}{\partial x} \left(1- \exp \left[ - \frac 1 \xi \left (V^\ell - V\right) \right]\right) \\ & + \sum_{\ell=1}^L\mathcal{J}^{\ell}g^{\ell*} \frac {\partial V^\ell}{\partial x} \end{align*}\end{split}\]

Notice how distorted intensities act like endogenous discount factors in this equation. The last two terms add flow contributions to pertinent Feynman-Kac equations via dot products with respect to \(m\). It is significant that these terms do not include derivatives of \(g^{\ell*}\) with respect to \(x\).

We may simulate our asset pricing representation of the partial derivatives of the value function by allowing the discounting term to adjust for the jump probabilities and hence becomes state dependent:

\[D_t \eqdef \exp\left( - \int_0^t\left[\delta + \sum_{\ell=1}^L\mathcal{J}^{\ell}(X_u)g^{\ell*}(X_u)\right]du\right),\]

In addition, three flow terms are discounted:

(11.19)\[\begin{split}\begin{align} \Phi_t^1 \eqdef & \delta \Lambda_t \cdot \frac {\partial U}{\partial x}(X_t) & \text{i)}\\ \Phi_t^2 \eqdef & + \xi \Lambda_t \cdot \sum_{\ell=1}^L \frac {\partial \mathcal{J}^{\ell}}{\partial x} (X_t) \left(1- \exp \left[ - \frac 1 \xi \left[V^\ell(X_t) - V(X_t) \right] \right]\right) & \text{ii)}\\ \Phi_t^3 \eqdef & + \Lambda_t \cdot \sum_{\ell=1}^L\mathcal{J}^{\ell}(X_t)g^{\ell*}(X_t) \frac {\partial V^\ell}{\partial x} (X_t) & \text{iii)} \\ \end{align}\end{split}\]

Its revealing to think of right side as providing three different sources of the marginal values. The contributions of \(V^{\ell} - V\) and \(\frac {\partial V^\ell}{\partial x}\) are to be expected because they help to quantify the consequences of potential jumps. We may further decompose terms ii) and iii) by the jump type \(\ell\) to assess which jumps are the most important contributors to the marginal valuations. Analogous representations can be derived for the \(\frac {\partial V^\ell}{\partial x}\)’s conditioned on each of the jumps occurring.

Notice that term ii) of formula (11.19) includes derivatives of the jump intensity with respect to the state of interest. In some examples, the jump intensities are constant or depend only on an exogenous state. In such cases the second term drops out and only the first and third terms remain. In some models of interesting, including the example that follows, the intensities depend on endogenous state variables, making term ii) of particular interest.

Since term iii) features the post jump marginal valuations, we may view this contribution as itself being forward looking, conditioned on the respective jump.

Decomposition II

The three terms \(\Phi_t^1\) (direct marginal utility contribution), \(\Phi_t^2\) (marginal impact of a jump), and $\Phi_t^3 (marginal value should a jump take place contribute three marginal flows term to the marginal valuation giving rise to a decomposition:

\[\frac {\partial V} {\partial x}(X_0)\cdot \Lambda_0 + \Delta_0 = V^1(X_0) + V^2(X_0) + V^3(X_0)\]

where each are constructed analogously as the initial marginal valuation but with the stochastic flows \(\Phi^1, \Phi^2,\) and \(\Phi^3\) respectively. Simulation-based methods can be used to compute these value contributions. They should be conducted under implied worst-case diffusion dynamics. With multiple jump components, we may further decompose these contributions based on the jump types \(\ell\).

11.3.6. Climate change example

[Barnett et al., 2024] use representations (11.19) to decompose their model-based measure of the social cost of climate change and the social value of research and development. In their analysis, there are two types of Poisson jumps. One is the discovery of a new technology and the other is the recognization of how curved the damage function is for more extreme changes in temperature. They allow for twenty possible damage curves, corresponding to twenty different jump outcomes.) The magnitude of damage curvature is revealed by a jump triggered by a temperature anomaly between 1.5 and 2.5 degrees celsius. While there are twenty one possible jump types, we group them into damage jumps (one through twenty) and a technology jump (twenty one). [Barnett et al., 2024] display the quantitative importance of a technology jump and a damage jump in contributing to the social value of research and development. The intensities for each of the twenty potential damage curve realizations and depend on a temperature anomaly state variable. Global warming increases the intensity. Temperature is an endogenous state variable as it depends on the cumulative emissions. The jump intensity for the technology discovery depends on an endogenous knowledge stock variable. Instantaneous investment in research and development enhance this stock in accordance to a production relation. The marginal valuations of two endogenous state variables are of particular interest. In what follows, we report analogous findings for the social value of research and development and the social cost of climate change. The latter is measured as the negative of the marginal value of temperature. We take the negative of the marginal value of climate change because warming induces a social cost (a negative benefit).

[Barnett et al., 2024] entertain misspecification possibilities for both the diffusion and jump risks. We report the implied drift distortions for the broadly-based capital stock evolution and the stock of knowledge evolution for two different values of \(\xi\) in Table 1. These distortions are reported per unit of standard deviation of the corresponding Brownian increment. Smaller values of \(\xi\) correspond to higher degrees of aversion, inducing larger in magnitude drift distortions.

	capital	knowledge stock
more aversion (\(\xi=.05\))	-0.184	-0.008
less aversion (\(\xi=.1\))	-0.096	-0.003

Table 1: Drift distortions for capital stock evolution and the knowledge stock evolution at the initial time period.

Figure 1 shows the uncertainty-adjusted jump time probability densities for a technology jump for a simplified version of the model in [Barnett et al., 2024]. This figure shows that the uncertainty adjustments shifts the probabilities towards delayed success as we make the fictitious planner more averse to uncertainty.

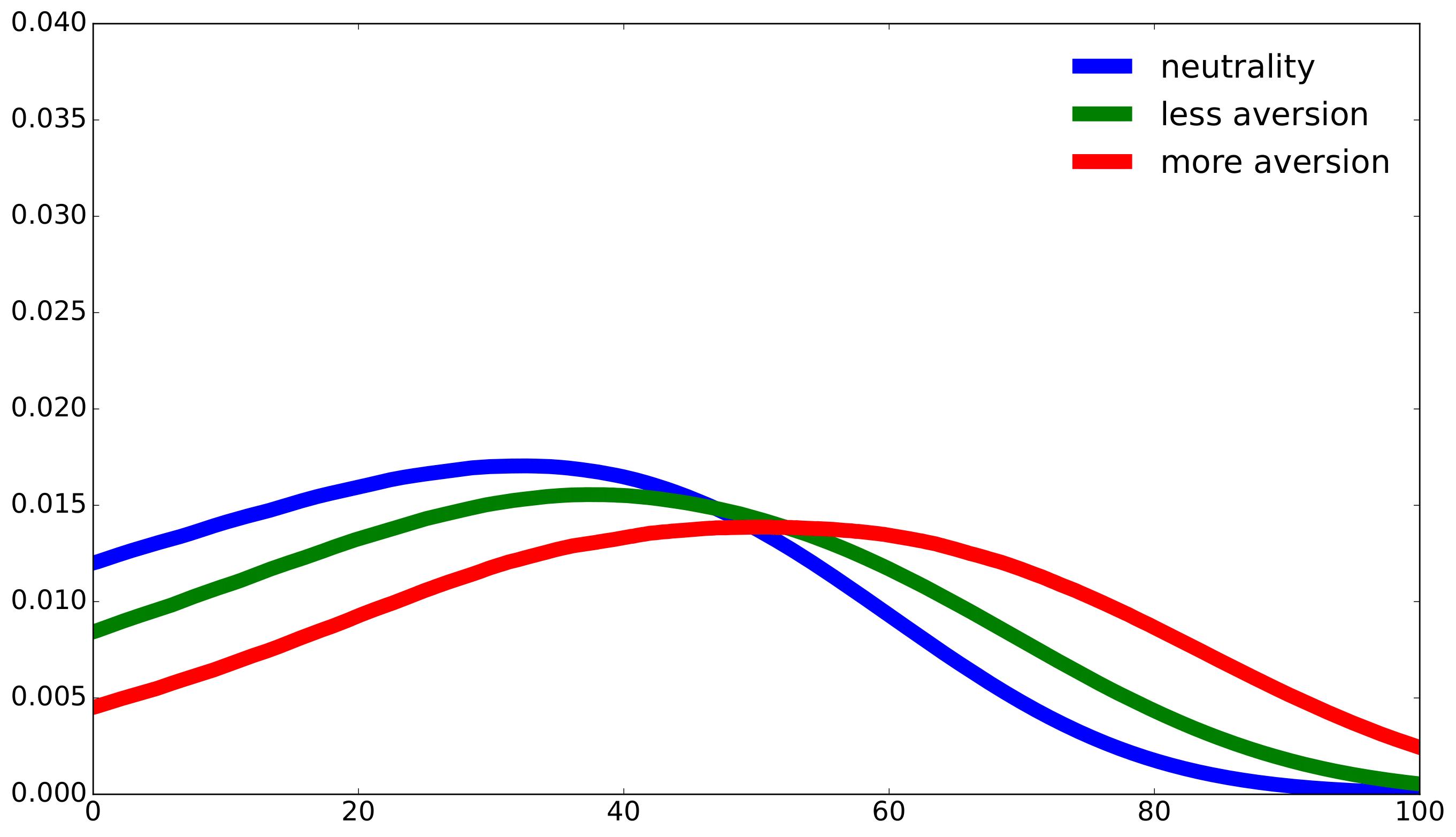
Figure 1: Densities for the time of the technology jump for different values of \(\xi\). For “neutrality”, \(\xi = \infty\)); for “less aversion”, \(\xi = .1\); and “more aversion”, \(\xi = .05\).

Table 2 shows results using Decomposition I applied to the marginal valuation of the knowledge stock variable (social value of research and development, SVRD) along with the associated investments. While the largest valuation contribution from knowledge stock state channel, the broadly based capital stock channel is also important contributor in contrast the temperature state channel. The magnitudes all increase under more aversion to misspecification as does the investment in R&D. Table 3 shows the analogous results for the social cost of climate change (SCCC) along with the emissions in the initial time period. The two capital channels contribute in opposite ways with the R&D channel decreasing the SCCC, as is to be expected. Again, magnitudes increase with the aversion to misspecification and emissions are modestly reduced.

\(\xi\)	capital	temperature	RD	sum	R&D investment	capital investment
\(\infty\)	14.2	-1.5	33.3	46.0	.008	.77
.10	24.6	-3.6	45.9	66.9	.015	.76
.05	35.9	-7.7	66.8	95.0	.028	.75

Table 2: Decomposition I of the Social Value of R&D. Each flow contribution has been divided by the marginal utility of (damaged) consumption. Both investments are expressed as a fraction of output.

\(\xi\)	capital	temperature	RD	sum	emissions
\(\infty\)	30.2	48.6	-22.4	56.4	9.28
.10	64.5	73.0	-49.3	88.2	9.02
.05	116.5	110.3	-87.3	139.4	8.66

Table 3: Decomposition I of the Social Cost of Climate Change. Each flow contribution has been divided by the marginal utility of (damaged) consumption.

Table 4 shows the result of Decomposition II applied to the SVRD along with the associated investments. Notice that flow term ii) (marginal impact of a technology jump) is the dominant contributor and that increases in the aversion make the R & D investment all the more attractive. There are two forces in play. While this aversion delays the prospect of success, the value consequence of the success are enhanced when the planner is more averse. The second force dominates in the results reported in this table. Table 5 shows that for values of \(\xi\) that are sufficiently low (misspecification aversion sufficiently high), the first force will dominate. Table 6 gives the comparable calculations for the SCCC. In this case there is a monotone relationship, with enhanced aversion leading inducing a large values for the SCCC and reductions in emissions.

\( \xi\)	flow i	flow ii	flow iii	sum	R & D investment	capital  investment
\(\infty\)	4.7 (10 %)	31.1 (68 %)	10.1 (22 %)	46.0	.008	.77
.10	9.1 (14 %)	41.9 (63 %)	15.9 (23 %)	66.9	.015	.76
.05	15.5 (16 %)	60.6 (64 %)	19.0 (20 %)	95.0	.028	.75

Table 4: Decomposition 2 of the Social Value of R&D. Three flow contributions to the SVRD for simplified model with only the jump technology. Each flow contribution has been divided by the marginal utility of (damaged) consumption. Both investments are expressed as a fraction of output.

\(\xi\)	SVRD	R&D investment
\(\infty\)	44.6	.008
.10	63.4	.015
.05	87.9	.028
.01	88.3	.030
.009	82.6	.026
.008	75.0	.021
.007	66.4	.017
.006	56.2	.012
.005	44.4	.007

Table 5: Social value of R&D (technology jump only) as a function of the robustness parameter, \(\xi\). The reported R&D investment is relative to output.

\(\xi\)	SCCC	emissions
\(\infty\)	59.3	9.28
.10	92.8	9.02
.05	151.1	8.66
.01	413.6	7.30
.009	421.9	7.23
.008	430.3	7.16
.007	438.2	7.07
.006	445.4	6.98
.005	451.1	6.87

Table 6: Social Cost of Climate Change (technology jump only) as a function of the robustness parameter, \(\xi\).

11.3.7. Footnote –>

---

[1]

[Cai et al., 2017]’s measurements are based on solutions to a planner’s problem that include explicit risk considerations. [Rennert et al., 2022] use a more modular approach to incorporate a wide variety of alternative sources of risk. [Barnett et al., 2025] more recent paper extends the analysis of [Barnett et al., 2020] to include social value of research and development.