8. Exploring Recursive Utility#
Authors: Jaroslav Borovicka (NYU), Lars Peter Hansen (University of Chicago) and Thomas J. Sargent (NYU) \(\newcommand{\eqdef}{\stackrel{\text{def}}{=}}\)
8.1. Introduction#
We explore the recursive utility preference specification of [Kreps and Porteus, 1978] and [Epstein and Zin, 1989] including versions of them proposed by [Hansen and Sargent, 2001] and [Anderson et al., 2003] that capture concerns about model misspecification as in. We deploy two distinct approximation approaches. One approach builds on a characterization by [Duffie and Epstein, 1992] and uses a continuous-time limiting approximation to a discrete-time specification in which underlying shocks are normally distributed, though our detailed derivations differ from those of [Duffie and Epstein, 1992]. We represent the limiting approximation with a Brownian motion information structure. Our second approximation m allows macroeconomic uncertainty to have first-order implications. We show how to explore model implications for (nonstandard) first- and second-order approximations to equilibria of dynamic stochastic models. We modify first- and second-order approximations routinely used in the macroeconomics literature in ways designed to focus on macroeconomic uncertainty. Our approximations apply to production-based macro-finance models with opportunities to invest in different kinds of capital. Both of our approximation approaches capture adjustments for uncertainty with a change in probability measure, one that differs from one that leads the so-called risk neutral distribution widely used to price derivative claims. Such a change of measure plays a big role in specifications of preferences like those in [Hansen and Sargent, 2001] and [Anderson et al., 2003] that build on a robust control literature initiated by [Jacobson, 1973] and [Whittle, 1981].
Our approximations allow macroeconomic uncertainty to have first-order implications. We assume risk averse economic decision makers with recursive utility preferences or closely related preferences that also express concerns about model misspecification. We show how to explore model implications for (nonstandard) first and second-order approximations to equilibria of dynamic stochastic models. We modify first and second order approximations routinely used in the macroeconomics literature in ways that focus on macroeconomic uncertainty. Our uncertainty adjustments are captured by a change in probability measure. Furthermore, our approximations apply to production-based macro-finance models with opportunities to invest in diverse forms of capital. We use this framework to advance our understanding of alternative preference specifications and their implications for production and asset pricing.
We extend work by [Schmitt-Grohé and Uribe, 2004] and [Lombardo and Uhlig, 2018] in ways that highlight consequences of uncertainty. We design approximations to make implied stochastic discount factors reside within an exponential linear quadratic class, a class that gives rise tractable formulas for asset valuation over alternative investment horizons. See, for instance, [Ang and Piazzesi, 2003] and [Borovička and Hansen, 2014]. The class is also useful for studying production-based macro-finance models with opportunities to invest in different forms of capital.
Note
We of course recognize that nonlinearities in some models are more accurately captured by global solution methods.
8.2. Recursive utility valuation process#
We construct continuation value and stochastic discount processes, important constituents of many dynamic stochastic models in macroeconomics and finance.
8.2.1. Basic recursion#
A homogeneous of degree one representation of recursive utility is
where
Value \(V_t\) defined in equation (8.1) is a homogeneous of degree one function of \(C_t\) and \(R_t\); equation (8.2) defines \(R_t\) as a homogeneous of degree one function of another function of \(V_{t+1}\).
In equation (8.1), \(0 < \beta < 1\) is a subjective discount factor and \({\frac 1 \rho}\) is the elasticity of intertemporal substitution, while \(\gamma\) in equation (8.2) describes attitudes towards risk.
Continuation values are determined only up to an increasing transformation. For computational and conceptual reasons, it is useful to work with the transformation \({\widehat V}_t = \log V_t\). Recursions for \({\widehat V}_t\) expressed in terms of the logarithm of consumption \({\widehat C}_t\) are
where
The right side of recursion (8.3) is the logarithm of a constant elasticity of substitution (CES) function of \(\exp({\widehat C}_t)\) and \(\exp({\widehat R}_t)\).
Remark 8.1
The limit of \({\widehat R}_t\) as \(\gamma\) approaches \(1\) is expected logarithmic utility:
We shall construct small noise expansions of \({\widehat V}_t\) and \({\widehat R}_t\) separately, then assemble them appropriately. Before doing so, we offer a reinterpretation of our recursions (8.3)-(8.4).
8.2.2. Preference for robustness#
When \(\gamma > 1\), (8.4) emerges as an indirect utility function for a robust control problem in which \(\frac 1 {\gamma - 1}\) serves as a penalty parameter on entropy of a baseline model relative to an alternative model. The penalty parameter constrains a set of alternative probability models that a decision maker considers when evaluating consumption processes. This interpretation of (8.4) as an indirect utilty function from a minimization problem originated in [Hansen and Sargent, 1995], which built [Jacobson, 1973] and [Whittle, 1981].
Let the random variable \(N_{t+1} \ge 0\) satisfy \({\mathbb E} \left( N_{t+1} \mid {\mathfrak A}_t \right) = 1\) so that it is a likelihood ratio. Think of replacing the expected continuation value \({\mathbb E} \left( {\widehat V}_{t+1} \mid {\mathfrak A}_t \right)\) by
where \(\xi\) is a parameter that penalizes departures of \(N_{t+1}\) from unity as measured by relative entropy. Conditional entropy relative to an alternative conditional probability induced by applying change of measure \(N_{t+1}\) is
The inequality follows from Jensen’s inequality because the function \(n \log n\) is convex. Relative entropy is evidently zero when \(N_{t+1} = 1\).
Relative entropy measures a discrepancy between two probability distributions. Think of \(N_{t+1}\) as a relative conditional likelihood ratio of an alternative model vis-a-vis a baseline model. Then \({\mathbb E} \left( N_{t+1} \log N_{t+1} \mid {\mathfrak A}_t \right)\) is an expected (conditional) log-likelihood ratio of the alternative model when the expectation is taken using the alternative probability model. A small expected log likelihood indicates a small discrepancy between two models, i.e., two probability distributions.
Remark 8.2
To solve minimization problem (8.5), we attach a Lagrange multiplier \(\ell\) to the conditional expectation constraint and form a Lagrangian that we want to minimize with respect to the random variable \(N\) and maximize with respect to \(\ell\). This extremization problem separates across states, so to minimze with respect to \(N\) we can solve a set of minimum problems
where \(n\) is a potential realization of \(N_{t+1}\) and \(v\) is a realization of \(V_{t+1}.\) First-order necessary conditions are:
which implies the minimizer
and the minimized objective
To determine \(\ell,\) we pose
whose first-order necessary condition is
The maximizing \(\ell\) is
and the minimized objective function is
The minimizing \(N_{t+1}\) is
The minimizer (8.6) of problem (8.5) evidently shifts probabilities toward low continuation values. [Bucklew, 2004] called this a stochastic version of Murphy’s law. Notice that the minimized objective satisfies
where earlier we described \({\widehat R}_t\) by equation (8.4) after we set \(\xi = {\frac 1 {\gamma - 1}} \).
It follows from (8.6) that
The random variable \(N_{t+1}^*\) will appear often below.
8.2.3. Stochastic discount factor process#
A stochastic discount factor (SDF) process \(S = \{ S_t : t \ge 0 \}\) describes a consumer’s attitudes about small changes in uncertainty. SDF processes have several uses. First, they contain shadow prices that tell how a consumer’s attitudes about uncertainty shape marginal valuations of risky assets. Second, they shape first-order necessary conditions for optimally choosing financial and physical investments. Third, they underlie tractable formulas for equilibrium asset prices. Fourth, they can help construct Pigouvian taxes that ameliorate externalities under uncertainty. Fifth, they can help evaluate effects of small (local) changes in government policies.
To deduce an SDF process, we positing that a date zero value of a risky date \(t\) consumption payout \(\chi_t\) is
To compute the ratio \( \frac {S_t}{S_0} \) that appears in formula (8.7) we evaluate the slope of an indifference curve that runs through both a baseline consumption process \(\{C_t\}_{t=0}^\infty\) and a perturbed consumption process
We think of \({\sf q}\) as parameterizing an indifference curve, so \(P_0({\sf q})\) expresses how much current period consumption must be reduced to keep a consumer on the same indifference curve after we replace \(C_t\) by \(C_t + {\sf q} \chi_t\). We set \(\pi_0^t(\chi_t)\) defined in equation (8.7) equal to the slope of that indifference curve:
For recursive utility, a one-period increment in the stochastic discount factor process is
where
and \(N_{t+1}^*\) induces the change of probability measure that equation (8.6) presents as the outcome of a robust valuation problem. We will use the second line in (8.8) in what follows. We will think of \(\beta\) as a subjective discount factor adjustment, \(N_{t+1}^*\) as a change-of-measure adjustment for uncertainty, and \(\exp\left({\widehat S}_{t+1} - {\widehat S}_t \right)\) as an adjustment for the elasticity of intertemporal substitution. We interpret the twisted transition probability measure induced by \(N_{t+1}^*\) as an adjustment for uncertainty in valuation.
The recursive structure of preferences makes the time \(t\) period stochastic discount factor \(\frac {S_t}{S_0}\) be the product of the respective one-period stochastic discount factor increments. Similarly, we can compound one-period transition uncertainty measures into multiple time-horizon measures of uncertainty.
Remark 8.3
To verify formula (8.8), we compute a one-period intertemporal marginal rate of substitution. Given the valuation recursions (8.3) and (8.4), we construct two marginal utilities familiar from CES and exponential utility:
From the certainty equivalent formula, we construct the marginal utility of the next-period logarithm of the continuation value:
where the \(+\) superscript is used to denote the next-period counterpart. In addition, the next-period marginal utility of consumption is
Putting these four formulas together using the chain rule for differentiation gives a marginal rate of substitution:
Now let \({\hat v}^+ = {\widehat V}_{t+1}\), \(c^+ = C_{t+1}\), \(C_t = c\) and \({\hat r} = {\widehat R}_t\) to obtain the formula for the one-period stochastic discount factor (8.8).
8.3. Continuous-time limit#
We now explore a continuous-time limit that approximates a discrete-time specification. Since we continue to work with normal shocks, the continuous-time counterpart to these shocks are Brownian increments. The continuation value in continuous time will evolve as:
for some drift (local mean), \(V_t \mu_t^V\) and some local shock exposure vector \(V_t \sigma_t^V\), where \(\{W_t : t \ge 0\}\) is a multivariate Brownian motion. The scaling for the local evolution coefficients by \(V_t\) is done for convenience, where the continuation value process is presumed to be positive. As in discrete time, it is convenient to work with the logarithm of the continuation value process (a strictly increasing transformation). The implied evolution is
where \({\hat \mu}_t = {\mu}_t^V - {\frac 1 2} \mid \sigma_t^V \mid^2.\) This adjustment follows from the well known Ito’s formula.
8.3.1. Discrete-time approximation#
To study the utility recursion, start with a discrete-time specification:
where \(\beta_\epsilon = \exp(- \delta \epsilon)\) and \(\delta>0\) is instantaneous subjective rate of discount. Consider the time derivative of the second recursion:
by local log normality. We turn now to the first recursion and compute time derivatives in three steps. First, we evaluate the term inside the logarithm as \(\epsilon\) tends to zero :
This term is in the denominator as implied by the derivative with respect to a logarithm. Second, we differentiate the term inside the logarithm with respect to \(\epsilon\) as contributed by \(\beta_\epsilon\):
Third, we differentiate the term inside the logarithm with respect to \(\epsilon\) as contributed by
Putting together the derivative components together gives:
Notice that this relation imposes a restriction across the local mean, \({\mu}_t^V\) and local variance, \( |\sigma_t^V|^2\) of the continuation value. [Duffie and Epstein, 1992] refer to \(\gamma\) as a variance multiplier where larger values of \(\gamma\) imply a more substantial adjustment for local volatility. As in discrete-time, the \(\rho = 1\) is interesting special case represented as;
8.3.2. Robustness to misspecification#
To investigate an aversion to model misspecification in continuous time, we now treat the distribution of \(\{W_t : t\ge0\}\) as uncertain. We allow for probability measures that entertain possible Brownian motions with local means or drifts that are history dependent.
We start by considering positive martingales \(\{ M^H_t : t \ge 0\}\) parameterized by
alternative \(\{ H_t : t \ge 0\}\) processes with the same dimension as the underlying Brownian motion.
The martingales have local evolutions:
and we initialize them at \(M_0^H = 1\). Observe that by applying Ito’s formula, \(\log M^H\) evolves as:
We use these martingales as relative densities or likelihood ratios.
Write the discrete-time counterpart as
Let \(w\) be a realized \(W_{t+\epsilon} - W_t\) and \(h\) be a realization \(H_t\). Then \(\log M_{t+\epsilon} - \log M_t\) contributes \( -{\frac \epsilon 2}h'h + h\cdot w \) to the log-likelihood. The standard normal density for \(\sqrt{\epsilon } \left(W_{t+\epsilon} -W_t\right)\) contributes \(-{\frac 1 \epsilon} w'w - \log (2 \pi \epsilon)\). Put there two components together, we have a log-likelihood:
The altered conditional density has mean \(\epsilon h\), which is the realized value of \(\epsilon H_t\) with the same conditional covariance matrix as before. Moreover, the conditional expectation of
which measures the statistical divergence or relative entropy between original and altered conditional probabilities.
For the continuous-time limit, under the \(H\) change of probability measure:
where \({\widetilde W}^H\) is a standard Brownian motion. Thus the potential changes of probability measures induce a local means or drift \(H\) processes to the Brownian motion. The continuous-time counterpart to conditional relative entropy at time \(t\) is \({\frac 1 2} \left| H_t \right|^2.\)
We may justify focusing on drift distortions for Brownian increments because of our imposition of absolute continuity of the alternative probabilities with respect to the baseline specification of a multivariate standard Brownian motion. This is an implication of the Girsanov Theorem.
We are now in a position to deduce a robustness adjustment in continuous time. Consider formula (8.10) when \(\gamma = 1\) modified for a potential change in the probability measure
Modify this equation to include minimization over \(H_t\) subject to a relative entropy penalty \(\frac \xi 2 |H_t|^2:\)
The minimizing solution is
with a minimized objective
Notice that this agrees with formula (8.10) for \(\gamma - 1= 1/\xi\). The explicit link is entirely consistent with our discrete-time equivalence result. By taking the continuous-time limit, we are able to focus our misspecification analysis on changing local means of the underlying Brownian increments.
8.3.3. Uncertainty pricing#
For the purposes of valuation, we compound the equilibrium version of \(\{ H_t^* : t \ge 0\}\) to give a exponential martingale:
provided that the constructed process is a martingale.[1] With this construction we interpret \(-H_t^*\) as the vector of local uncertainty prices that give compensations for exposure to Brownian increment uncertainty. These compensations are expressed as changes in conditional means under the baseline distribution as is typical in continuous-time asset pricing.
8.4. Small noise expansion of dynamic stochastic equilibria#
We next consider a different type of characterization that sometimes gives good approximations for dynamic stochastic equilibrium models. While the approximations build from derivations in [Schmitt-Grohé and Uribe, 2004] and [Lombardo and Uhlig, 2018], and we extend them in a way that features the uncertainty contributions more prominently and are reflected even in first-order contributions. By design, the implied approximations of stochastic discount factors used to represent market or shadow values reside within the exponential linear quadratic class. This class is known to give tractable formulas for asset valuation over alternative investment horizons. See, for instance, [Ang and Piazzesi, 2003] and [Borovička and Hansen, 2014]. Moreover, they are applicable to production-based macro-finance models with investment opportunities in alternative forms of capital.
While these approximations are tractable for the reasons described, researchers may be concerned about some more fundamental aspects of uncertainty that are disguised by these methods. Indeed, for some models nonlinearities are more accurately captured by global solution methods. Nevertheless, the approximations still provide further understanding of the preferences and their implications for asset pricing in endowment and production economies.
8.4.1. Approximate state dynamics#
We follow [Lombardo and Uhlig, 2018] by considering the following class of stochastic processes indexed by a scalar perturbation parameter \(\mathsf{q}\):[2]
Here \(X\) is an \(n\)-dimensional stochastic process and \(\{W_{t+1}\}\) is an i.i.d.~normally distributed random vector with conditional mean vector \(0\) and conditional covariance matrix \(I\). We parameterize this family so that \({\sf q} = 1\) gives the model of interest.
We denote a zero-order expansion \({\sf q} = 0\) limit as:
and assume that there exists a second-order expansion of \(X_{t}\) around \(\mathsf{q} = 0\):
where \(X_t^1\) is a first-order contribution and \(X_t^2\) is a second-order contribution. In other words, the stochastic processes \(X^j\), \(j=0,1,2\) are appropriate derivatives of \(X\) with respect to the perturbation parameter \({\sf q}\) evaluated at \({\sf q} = 0.\)
In the remainder of this chapter, we shall construct instances of the second-order expansion (8.13) in which the generic random variable \(X_t\) is replaced, for example, by the logarithm of consumption, a value function, and so on. I
Processes \(X_t^j, j=0, 1, 2\) have a recursive structure: first compute the stochastic process \(X_{t}^0,\) then the process \(X_{t}^1\) next (it depends on \(X_t^0\)), and finally the process \(X_{t}^2\) (it depends on both \(X_{t}^0\) and \(X_{t}^1\)).
In this chapter, we use a prime \('\) to denote a transpose of a matrix or vector. When we include \(x'\) in a partial derivative of a scalar function it means that the partial derivative is a row vector. Consistent with this convention, let \(\psi^i_{x'}\), the \(i^{th}\) entry of \(\psi_{x'}\), denote the row vector of first derivatives with respect to the vector \(x\), and similarly for \(\psi^i_{w'}\). Since \({\sf q}\) is scalar, \(\psi_{\sf q}^i\) is the scalar derivative with respect to \({\sf q}\). Derivatives are evaluated at \(X_t^0\), which in many examples is invariant over time, unless otherwise stated. This invariance follows when we impose a steady state on the deterministic system.
The first-derivative process obeys a recursion
that we can write compactly as the following a first-order vector autoregression:
We assume that the matrix \(\psi_x'\) is stable in the sense that all of its eigenvalues are strictly less than one in modulus.
It is natural for us to denote second derivative processes with double subscripts. For instance, for the double script used in conjunction with the second derivative matrix of \(\psi^i\), the first subscript without a prime (\('\)) reports the row location; second subscript with a prime (\('\)) reports the column location. Differentiating recursion (8.14) gives:
Recursions (8.14) and (8.15) have a linear structure with some notable properties. The law of motion for \(X^0\) is deterministic and is time invariant if (8.11) comes from a stationary \(\{X_t\}\) process. The dynamics for \(X^2\) are nonlinear only in \(X^1\) and \(W_{t+1}\). Thus, the stable dynamics for \(X^1\) that prevail when \(\psi_x\) is a stable matrix imply stable dynamics for \(X^2\).
Remark 8.4
Perturbation methods have been applied to many rational expectations models in which partial derivatives of \( \psi \) with respect to \(\mathsf{q}\) are often zero.[3] However, derivatives of \( \psi \) with respect to \(\mathsf{q}\) are not zero in production-based equlibrium models with the robust or recursive utility specifications that we shall study here.
Let \(C\) denote consumption and \({\widehat C}\) the logarithm of consumption. Suppose that the logarithm of consumption evolves as:
Approximate this process by:
where
In models with endogenous investment and savings, the consumption dynamics and some of the state dynamics will emerge as the solution to a dynamic stochastic equilibrium model. We use the approximating processes (8.13) and (8.16) as inputs into the construction of an approximating continuation value process and its risk-adjusted counterpart for recursive utility preferences.
8.5. Incorporating preferences with enhanced uncertainty concerns#
To approximate the recursive utility process, we deviate from common practice in macroeconomics by letting the risk aversion or robust parameter in preferences depend on \({\sf q}:\)
The aversion to model misspecification or the aversion to risk moves inversely with the parameter \({\sf q}\) when we embed the model of interest within a parameterized family of models. In effect, the variable \({\sf q}\) is doing double duty. Reducing \({\sf q} > 0\) limits the overall exposure of the economy to the underlying shocks. This is offset by letting the preferences include a greater aversion to uncertainty. This choice of any expansion protocol has significant and enlightening consequences for continuation value processes and for the minimizing \(N\) process used to alter expectations. It has antecedents in the control theory literature, and it has the virtue that implied uncertainty adjustments occur more prominently at lower-order terms in the approximation.
8.5.1. Order-zero#
Write the order-zero expansion of (8.3) as
where the second equation follows from noting that randomness vanishes in the limit as \(\mathsf{q}\) approaches \(0\).
For order zero, write the consumption growth-rate process as
The order-zero approximation of (8.3) is:
We guess that \({\widehat V}_t^0 - {\widehat C}_t^0 = \eta_{v-c}^0\) and will have verified the guess once we solve:
This equation implies
Equation (8.17) determines \( \eta_{v - c}^0\) as a function of \(\eta_c^0\) and the preference parameters \(\rho, \beta\), but not the risk aversion parameter \(\gamma\) or its robust counterpart \(\xi\). Specifically,
In the limiting \(\rho =1\) case,
8.5.2. Order-one#
We temporarily take \({\widehat R}_t^1 - {\widehat C}_t^1\) as given. We construct a first-order approximation to the nonlinear utility recursion (8.3)
where
Notice how the parameter \(\rho\) influences the weight \(\lambda\) when \(\eta_c \neq 0\), in which case the log consumption process displays growth or decay. The condition \(\lambda <1\) restricts the subjective discount rate, \(-\log \beta,\) relative to the consumption growth rate \(\eta_c\) since
When \(\rho < 1\), the subjective discount rate has a positive lower bound in contrast to the case in which \(\rho \ge 1\).
To facilitate computing some useful limits we construct:
which we assume remain well defined as \({\sf q} \) declines to zero, with limits denoted by \({\widetilde V}_t^0\) and \({\widetilde R}_t^0\). Importantly,
Taking limits as \({\sf q}\) declines to zero:
Subtracting \({\widehat C}_t^1\) from both sides gives:
Substituting formula (8.22) into the right side of (8.19) gives the recursion for the first-order continuation value:
Remark 8.5
We produce a solution by “guess and verify.” Suppose that
It follows from (8.23) that
Deduce the second equation by observing that
is distributed as a log normal. The solutions to equations (8.25) are:
The continuation value has two components. The first is:
and the second component is a constant long-run risk adjustment given by:
This second term is the variance of
conditioned on \({\mathfrak A}_t\) scaled by \(\frac {\lambda(1 - \gamma_0)} {2(1 - \lambda)}\).
Remark 8.6
The formula for \( \upsilon_1 \) depends on the parameter \( \rho \). Moreover, \( \upsilon_1 \) has a well-defined limit as \( \lambda \) tends to unity as does the variance of (8.26). This limiting variance:
converges to the variance of the martingale increment of \({\widehat C}^1\).
Remark 8.7
Consider the logarithm of the uncertainty-adjusted continuation value approximated to the first order. Note that from (8.24),
Substitute this expression into formula (8.22) and use the formula for the mean of random variable distributed as a log normal to show that
Associated with the first-order approximation, we construct:
Equation (8.22) is a standard risk-sensitive recursion applied to log-linear dynamics. For instance, see [Tallarini, 2000]’s paper on risk-sensitive business cycles and [Hansen et al., 2008]’s paper on measurement and inference challenges created by the presence of long-term risk.[4] Both of those papers assumed a logarithmic one-period utility function, so that for them \(\rho=1.\) Here we have instead obtained the recursion as a first-order approximation without necessarily assuming log utility. Allowing for \(\rho\) to be different than one shows up in both the order zero and order one approximations, as reflected in (8.18) and (8.23), respectively. In accordance to (8.23), for the first-order approximation the parameter \(\lambda = \beta\) when \(\rho = 1\). But otherwise, it is different. Equation (8.22) also is very similar to a first-order approximation proposed in [Restoy and Weil, 2011]. Like formula (8.22), [Restoy and Weil, 2011] allow for \(\rho \ne 1.\) In contrast, our equation has an explicit constant term coming from the uncertainty adjustment, and we have explicit formula for \(\lambda\) that depends on preference parameters and the consumption growth rate.
Remark 8.8
The calculation reported in Remark 8.7 implies that
As a consequence, under the change in probability measure induced by \(N_{t+1}^0,\) \(W_{t+1}\) has a mean given by
and with the same covariance matrix given by the identity. This is an approximation to robustness adjustment expressed as an altered distribution of the underlying shocks. It depends on \(\gamma_o - 1 = {\frac{1}{\xi_o}}\) as well as the state dynamics as reflected by \(\upsilon_1\) and by the shock exposure vectors \(\psi_{w'}\) and \(\kappa_{w'}\). As we will see, this change of measure plays a role in the higher-order approximation, but it also gives a low-order representation of the implied shadow or market one-period compensation for exposure to uncertainty. It captures the following insight from “long-run risk” models: investor concerns of long-term uncertainty impacts short-term asset valuation. In contrast to the “long-run risk” literature, our analysis opens the door to a different interpretation. Instead of aversion to risk it reflects an aversion to the misspecification of to models or simplified perspectives on macroeconomic dynamics.
As we noted in Remark Remark 8.6, \(\left( {\upsilon_1}'\psi_{w'} + \kappa_{w'} \right) W_{t+1}\) is approximately the martingale component of the logarithm of consumption when \(\lambda\) is close to one. In section:var we showed that the variance of this component is challenging to estimate, a point originally made by [Hansen et al., 2008]. This finding is part of the reason that we find it important to step back from rational expectations and limit investors confidence in the models they use for decision making.
8.5.3. Order two#
Differentiating equation (8.3) a second time gives:
Equivalently,
Rewrite transformations (8.20) and (8.21) as
Differentiating twice with respect to \({\sf q}\) and evaluated at \({\sf q} = 0\) gives:
Differentiating (8.21) with respect to \({\sf q}\) gives:
and thus
where subtracting \({\widehat C}_t^2\) from \({\widehat R}_t^2\) gives:
Substituting this formula into (8.27) gives:
Even if the second-order contribution to the consumption process is zero, there will be nontrivial adjustment to the approximation of \({\widehat V} - {\widehat C}\) because \(\left( {\widehat R}^1 - {\widehat C}^1 \right)^2\) is different from zero. This term vanishes when \(\rho = 1,\) and its sign will be different depending on whether \(\rho\) is bigger or smaller than one.
8.6. Stochastic discount factor approximation#
We approximate \(\left[{\widehat S}_{t+1} - {\widehat S}_{t} \right]\) in formula (8.8) as
where
We now consider two different approaches to approximating \(N_{t+1}^*\).
8.6.1. Approach 1#
Write
Form the ``first-order’’ approximation:
We combine a first-order approximation of \(\log N_{t+1}^*\) with a second-order approximation of \({\widehat S}_{t+1} - {\widehat S}_t\):
which preserves the quadratic approximation of \(\log S_{t+1} - \log S_t.\). Note that If we were to use a second-order approximation of \(N_{t+1}^*\), it would push us outside the class of exponentially quadratic stochastic discount factors.
8.6.2. Approach 2#
Next consider an alternative modification of Approach 1 whereby:
and \(\log {\widetilde N}_t\) is used in conjunction with
By design, this approximation of \(N_{t+1}^*\) will have conditional expectation equal to one in contrast to the approximation used with Approach 1. With a little bit of algebraic manipulation, it may be shown that this approximation induces a distributional change for \(W_{t+1}\) with a conditional mean that is affine in \(X_{t+1}\) and an altered conditional variance matrix that is constant over time.
To understand better this choice of approximation, consider the family of random variables (indexed by \({\sf q}\))
The corresponding family of exponentials has conditional expectation one and the \({\sf q} = 1\) member is the proposed approximation for \(N_{t+1}^*.\) Differentiate the family with respect to \({\sf q}\):
Thus this family of random variables has the same first-order approximation in \({\sf q}\) as the one we derived previously for \(\log N_{t+1}^*\).
As a change of probability measure, this approximation will induce state dependence in the conditional mean and will alter the covariance matrix of the shock vector. We find this approach interesting because it links back directly to the outcome of the robustness formulation we described in Section 3.1.
8.7. Solving a planner’s problem with recursive utility#
The [Bansal and Yaron, 2004] example along with many others building connections between the macro economy and asset value take aggregate consumption as pre-specified. As we open the door to a richer collection of macroeconomic models, it becomes important to entertain more endogeneity, including investment and other variables familiar to macroeconomics.
Write a triangular system with stochastic growth as:
where \(D_t\) is a date \(t\) decision vector for the planner. Define \({\widehat G}_t = \log G_t.\) In addition, we impose
where the first equation is a vector of static constraints and the second constructs the measure of consumption that enters preferences.
We extend the approximations by using a co-state formulation. There are two essentially equivalent interpretations of these co-states. One is they function as a set of Lagrange multipliers on the state evolution equations. The other is that they are partial derivatives of value functions. The co-state equations are forward-looking, linking next period’s co-state vector to this period’s co-state vector. Given the recursive utility structure, we must include the implied value functions in the computations as they enter the relations of interest.
The first-order conditions for \(D\) are:
where \(MX_{t+1}\) and \(MG_{t+1}\) are the co-states, or the implicit multipliers one for each the state evolutions and \(MS_t\) is a multiplier on the first static constraint in (8.32). Recall that \(N_{t+1}^* = \exp\left[ (1-\gamma) \left({\widehat V}_{t+1} - {\widehat R}_t \right) \right]\) used for making an uncertainty adjustment in valuation.
In addition, we solve a forward-looking co-state equation given by
The approximation formulas, (8.22), (8.23), (8.28), (8.29), that we deduced previously for \({\widehat V}_t - {\widehat C}_t\) and \({\widehat R}_t - {\widehat C}_t\) have and immediate counterparts for \({\widehat V}_t - {\widehat G}_t\) and \({\widehat R}_t - {\widehat G}_t\), from which can build an approximation of \( {\widehat R}_t - {\widehat V}_t.\)
From recursive utility updating equation:
Dividing by both sides of the equation by \(\exp\left[ (1 - \rho ) {\widehat V}_t\right] \) gives
From the relation, we see that \(MG_t=1\) for \(t \ge 0\) satisfies the second block of co-state equation (8.34). In fact, this is the solution of interest.
8.7.1. An example economy with long-run uncertainty#
Consider an AK model with recursive utility and adjustment costs.
The exogenous state dynamic capture both long-run uncertainty in the mean growth rate and the overall volatility in the economy.
The state variable, \(Z_{2,t}\) is included to capture stochastic volatility. The discrete-time dynamics for \(\{\exp(Z_{2,t}) \}\) approximate a continuous-time version of what is called a square root process due to Feller. Let
With these exogenous dynamics, we obtain the following zero and first-order approximations:
and
We impose the resource constraint:
The endogenous state dynamics are given by:
where \({\widehat K}_t = \log K_t = {\widehat G}_t\). The planner choice variable \(D_t = \left( \frac{C_t}{K_t}, \frac{I_t}{K_t} \right)\). Rewrite the current-period resource constraints as:
Express the first-order conditions for the consumption-capital and investment-capital ratios as:
It is convenient to rewrite the first-order conditions for the consumption-capital ratio as:
which in turn implies that
More generally, we will seek to approximate \(\log MS_t\), as we expect the multiplier \(MS_t\) to be positive.
Notice that these first-order conditions do not depend on the co-state process \(\{MX_t : t \ge 0 \}\). We may solve this planner’s problem using (8.37) and up-dating the continuation value processes and its uncertainty-adjusted counterpart until convergence. When \(\rho = 1\), \({\widehat R}_t - {\widehat G}_t\) drops out of the first-order conditions and both components of \(D_t\) are constant since
When \(\rho \ne 1\), \(D_t\) depends on the exogenous state \(X_t\).
8.7.2. First-order approximation when \(\rho=1\)#
We obtain the following zero and first-order approximations for the exogenous dynamics:
and
The first-order conditions for \(D_{2,t}\) imply that:
Solving for \(D\) gives:
which is independent of the state, as should be expected since \(\rho = 1.\) From the capital evolution it follows from the order zero approximation is
The order one approximation is then:
Stochastic volatility, as in the [Bansal and Yaron, 2004] model of consumption dynamics, will be present in the second-order approximation.
8.7.3. Second-order approximation when \(\rho = 1\)#
We next consider the second-order approximations. The second-oder approximation for \(\{ Z_{2,t}\}\) does not contribute to the planner’s solution or to the implied shadow prices and thus we drop it from the analysis. For the remaining two state variables, we find that
where we previously noted that \(\{ Z_{2,t}^1\}\) evolves as first-order autoregression.
The combined approximation for \({\sf q}=1\) uses:
The approximate dynamics for the exogenous states remains the same for \(\rho \ne 1,\) but the solution for \(D^*\) becomes state dependent and the approximate dynamic evolution for capital is altered.
8.7.4. Shock elasticities#
We use the shock elasticities to explore pricing implications of this recursive utility specification. In what follows, we use exponential/linear/quadratic implementation by [Borovička and Hansen, 2014] and by [Borovička and Hansen, 2016] with the parameter configuration given in Table 1 of [Hansen et al., 2024]. This latter reference combines inputs from other sources including [Schorfheide et al., 2018] and [Hansen and Sargent, 2021].
Fig. 8.1 gives the shock exposure elasticities for consumption to each of the three shocks. They can be interpreted as nonlinear local impulse responses for consumption (in levels not logarithms). The elasticities for the growth rate shock and the stochastic volatility shock start small and increase over the time horizon as dictated by the persistence of the two exogenous state variable processes. The elasticities for the direct shock to capital are flat over the horizon as to be expected since the shock directly impacts log consumption in a manner that is permanent. Notice that while elasticities for the volatility shock are different from zero, their contribution is much smaller than the other shocks. Stochastic volatility does induce state dependence for the other elasticities as reflected by the quantiles.[5]
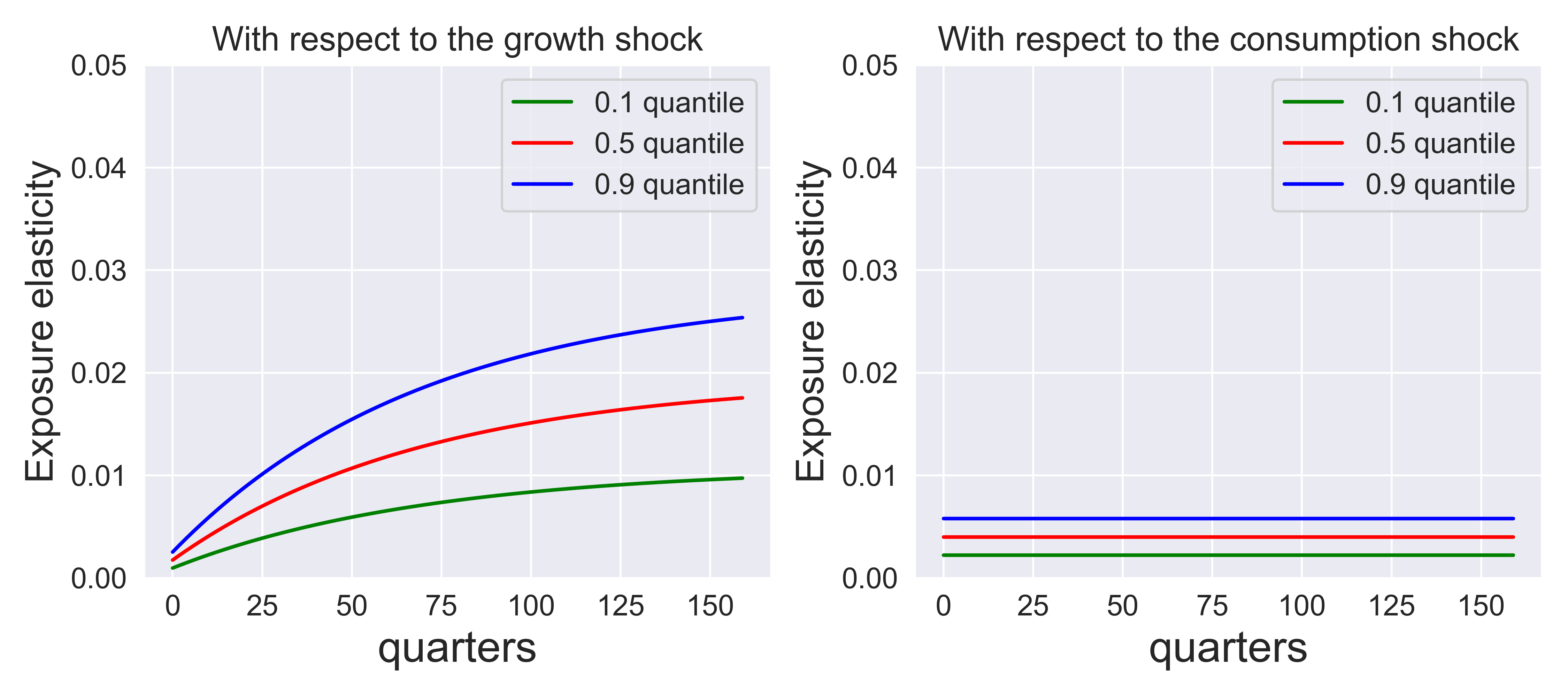
Fig. 8.1 Exposure elasticities for three shocks. \(\rho = 1, \gamma = 8,\) \(\beta = .99.\)#
Fig. 8.2 gives the shock price elasticities for growth-rate shock when \(\rho = 1\) and \(\gamma = 8\). Stochastic volatility induces state dependence in these plots as reflected by the quantiles. The recursive utility preferences are forward-looking as reflected by the continuation-value contribution to the one-period increment to the stochastic discount factor process (see (8.8)). This forward-looking contribution is reflected in shock price elasticities that are relatively flat for the growth rate shock as is evident from the second column. The shock price elasticity that is induced by uncertainty alone is flat since because the associated multiplicative functional is a martingale.[6]
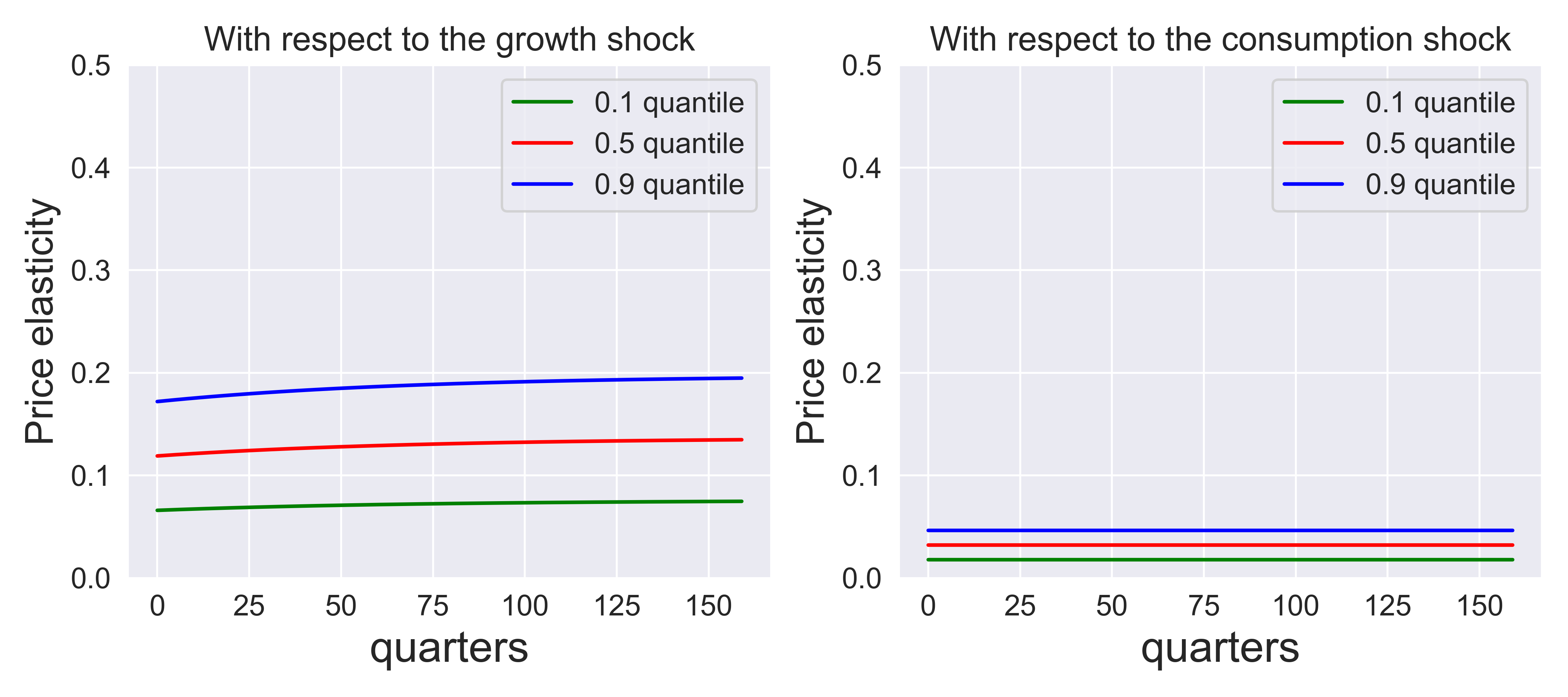
Fig. 8.2 Price elasticities for three shocks. \(\rho = 1, \gamma = 8,\) \(\beta = .99.\)#
Fig. 8.3 and Fig. 8.4 provide the analogous plots for \(\rho = 2/3, 3/2.\) Fig. 8.5 sets \(\rho=\gamma = 8\) which corresponds to preferences that are time separable. The forward-looking component to the stochastic discount factor is shut down as is evident from formula (8.8). Now the shock price elasticities and shock exposure elasticities show a very similar trajectory except that the shock price elasticities are about eight times larger.
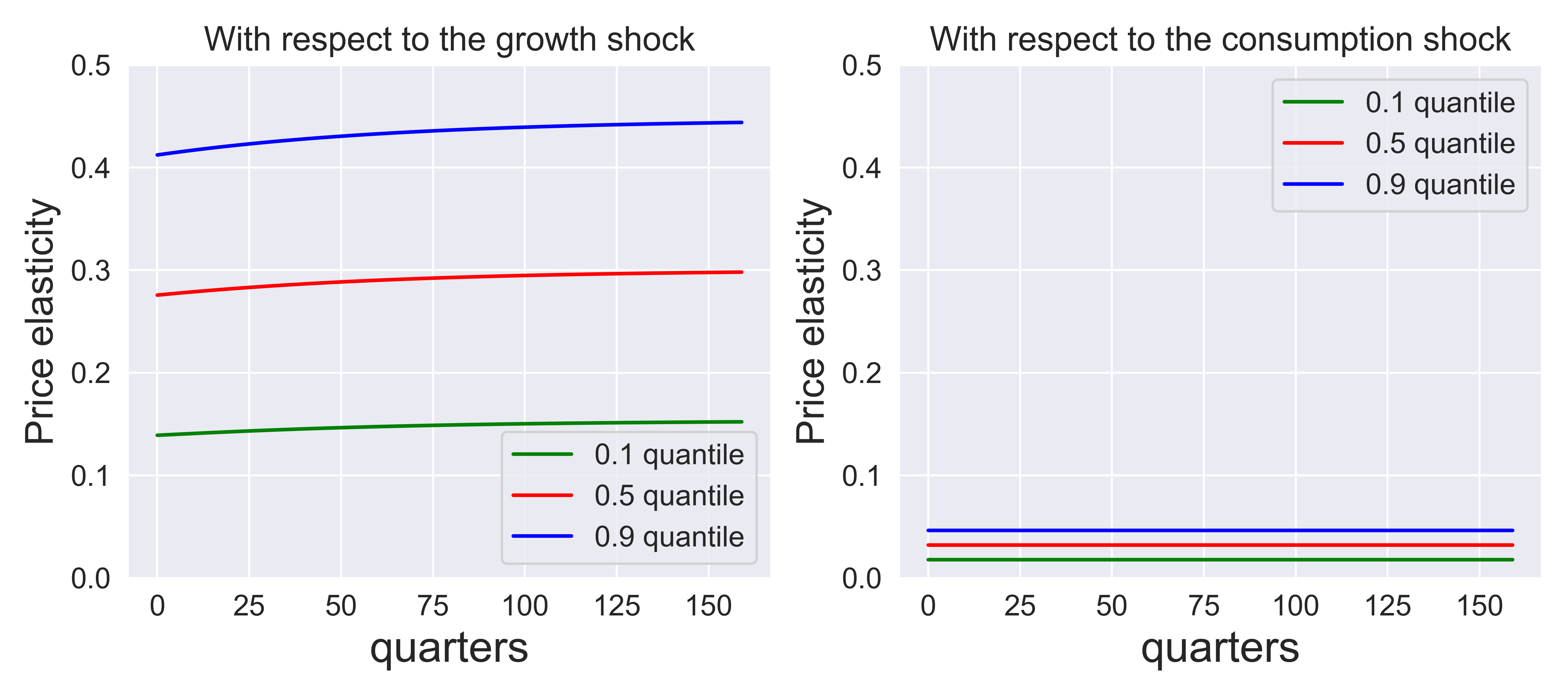
Fig. 8.3 Price elasticities for three shocks. \(\rho = 2/3, \gamma = 8,\) \(\beta = .99.\)#
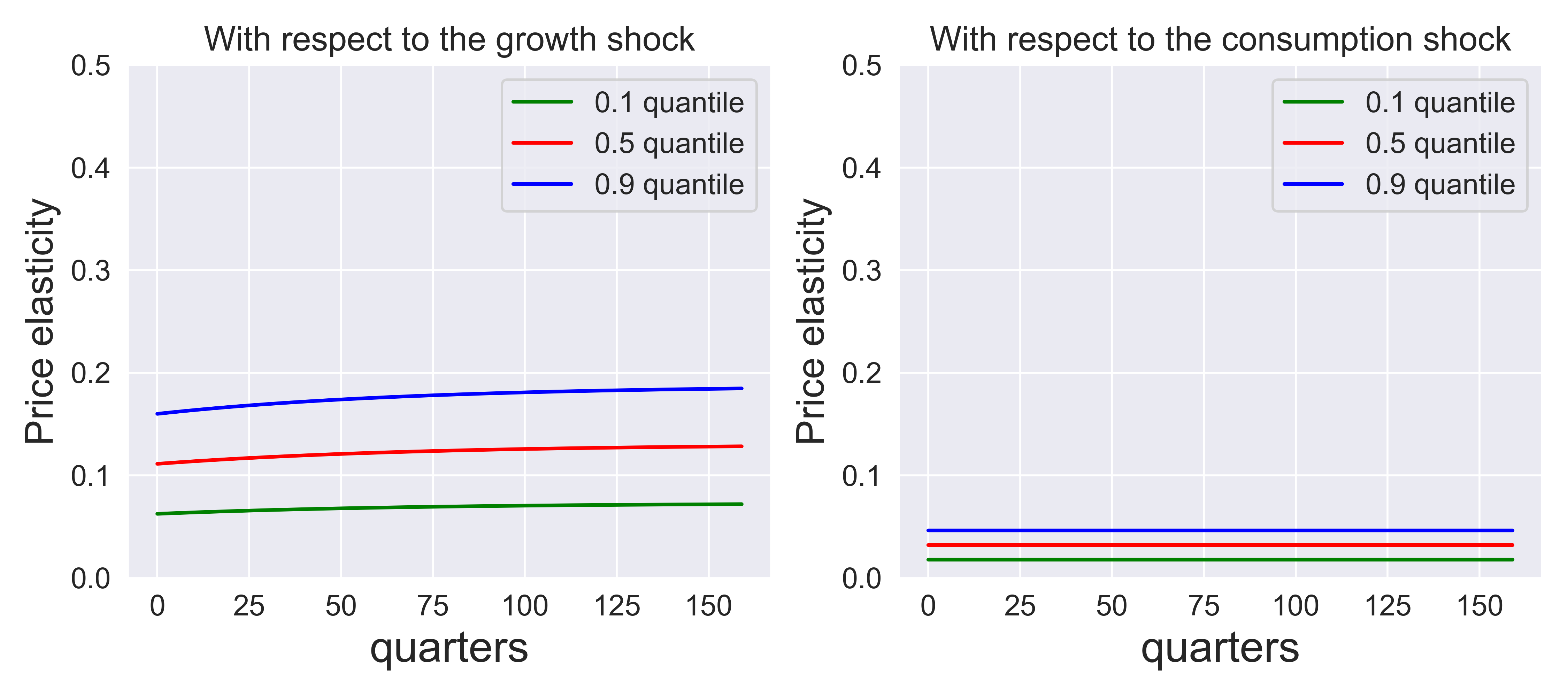
Fig. 8.4 Price elasticities for three shocks. \(\rho = 3/2, \gamma = 8,\) \(\beta = .99.\)#
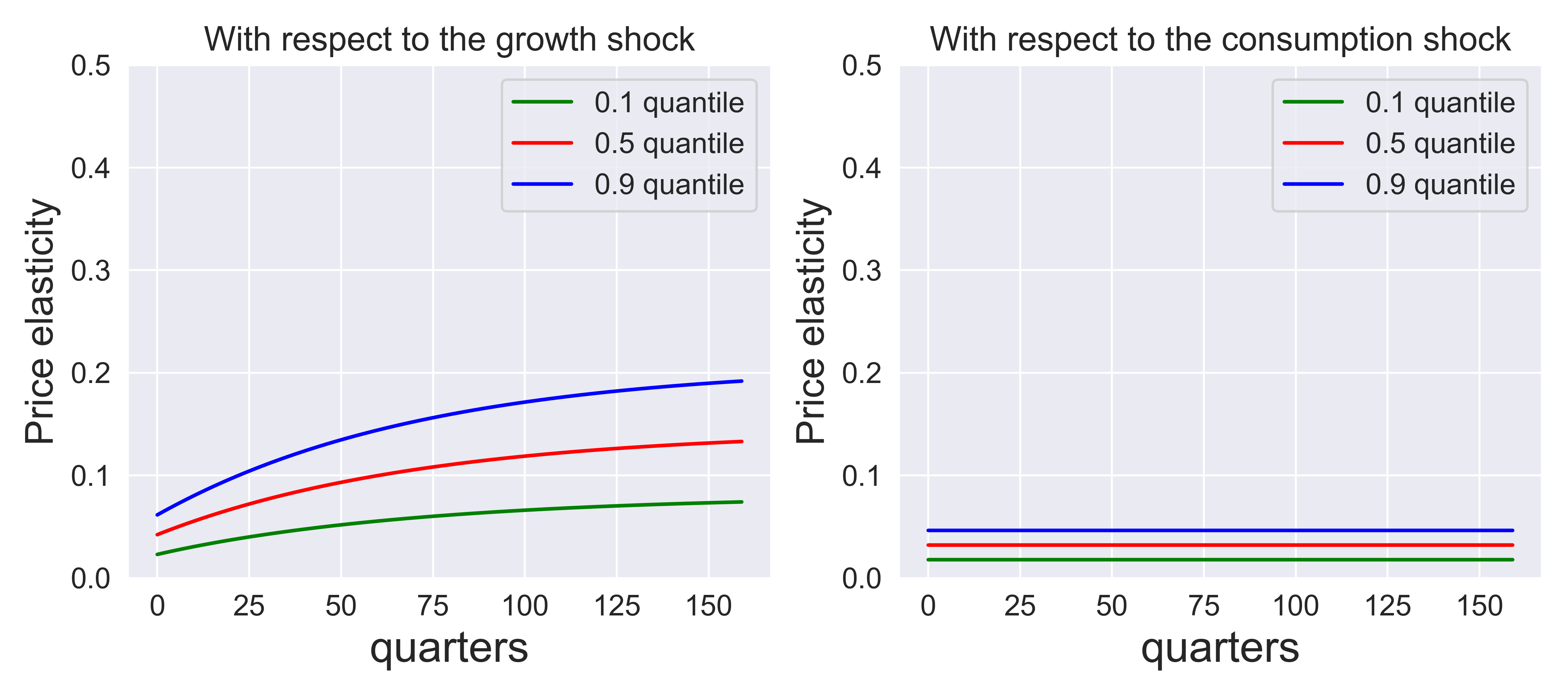
Fig. 8.5 Price elasticities for three shocks. \(\rho = 8, \gamma = 8,\) \(\beta = .99.\)#
8.7.5. An alternative model of intertemporal substitution/complementarity.#
We now extend the preference specification of the consumers in the AK model of Section 8.7.1 to explore implications of time nonseparability in preferences. We are motivated to do so by rather substantial previous literetaure. An important earlier contributor is [Ryder and Heal, 1973], who solve a social planner’s problem with stochastic growth. [Sundaresan, 1989], [Constantinides, 1990], [Heaton, 1995], and [Hansen et al., 1999] consider asset pricing implications with internal habit persistence. These papers essentially explore decentralizations of the planner’s problem. The latter paper considers simultaneously a recursive robustness specification as we will do here, although for a different model specification.
To accomplish this, we introduce an additional state variable, which we will call the habit stock, \(H_t\). This stock evolves as:
where \(\nu_h > 0\) is a depreciation rate. We think of this new investment = \(I_{h,t}\) as measured consumption.
Notice that the sum of the coefficients on the right side of the evolution equation sum to one. This allows us to interpret \(H_{t+1}\) as a geometric average of current and past values of measured consumption.
We write evolution equation in logarithms as
For numerical purposes, we transform this equation to be:
where we treat \(\log H_{t} - \log K_t\) as one of the components of \(X_t\) and we substitute the evolution of \(\log K_{t+1}\) to depict the evolution of this component. As previously, \({\widehat G}_t = \log K_t\).
We impose the output constraint as:
where \(I_{k,t}\) is the investment in the capital stock. Analogous to previous formulation, we transform this equation to be:
where \(\frac {I_{h,t}}{K_t} \) and \(\frac {I_{k,t}}{K_t}\) are the two components of \(D_t\).
What enters the utility function each date inside the recursive utility preference specification is the CES aggregate:
for \(\tau \ge 0\). This specification captures a form of intertemporal complementarity and intertemporal substitution in preferences. In static demand theory, \(\tau = 0\) implies perfect substitutes, and when \(\tau > 1\), the preferences display a form of complementarity as reflected in the cross price effects on demand. In the limiting case when \(\tau\) approaches \(+\infty\), preferences treat the two inputs as perfect complements and consumed in fixed proportions. There is a different notion of intertemporal complementarity as originally defined by [Ryder and Heal, 1973]. Under this notion, increasing \(H_t\), keeping \(I_{h,t}\) fixed should decrease \(C_t\). (They impose other restrictions.) This form of intertermporal complementarity can instead be captured by letting \(\lambda < 0\). Effectively, \(H_t\) is a “bad’’ not a “good,’’ in the CES aggregator. Setting \(0 < \lambda \le 1\) captures a form of consumption durability.
For computational purposes, we divide both sides of (8.38)`by \(K_t\) and take logarithms:
Consistent with the habit-persistence literature, we allow the parameter \(\lambda\) to be negative. When \(\tau\) is one, this becomes a Cobb-Douglas specification:
Remark 8.9
The asset pricing literature often features the computationally more challenging case in which \(\tau = 0.\) and \(\lambda < 0\). The local approximation methods we describe here could give particularly poor approximations for this parameter configuration.
For simplicity, consider the case in which \(\rho = \tau = 1\). Recall that \(\rho\) also impacts intertemporal substitution in preferences so by setting it to one we feature the novel contribution coming from this dynamic specification of preferences. The first-order conditions for \(D_t \) are:
Consider now the special case in which \(\lambda = 0.\) In the case the co-state \(MX_{t+1}\) should be zero. From the first-order conditions for \(D_{1,t}\), we find that
More generally,
This depicts the marginal value of \(MS_t\) in terms of both a current marginal utility contribution and a forward-looking piece coming from the planner internalizing the intertemporal contribution to preferences. We choose to use \(I_{h,t}\) as the date \(t\) numeraire instead of \(C_t\), as the former is measured consumption. In light of this choice, the logarithm of the one-period stochastic discount factor is
In our calculations, we approximate \(\log MS_t\) since it enters this formula for the logarithmic stochastic discount factor construction.
Figure Fig. 8.6 explores the median exposure elasticities for the investment-capital ratio as a function of the parameter \(\lambda\). Recall that these elasticities can be viewed as local impulse responses. The responses are different for the two shocks. For the growth-rate shock, with habit persistence (\(\lambda=1\)), there is an immediate decline followed by an eventual increase. In contrast, for durability (\(\lambda = .5)\) just the opposite happens. Given the restriction on output, the consumption/capital ratios have an offsetting response. For the direct shock to the technology, with habit persistence, the investment-capital ratio increases and monotonically declines to zero as a function of the investment horizon. Again, under consumption durability, the response is essentially the mirror image of this. Figure Fig. 8.7 provides the \(.1\) and \(.9\) quantiles as induced by stochastic volatility for the two shocks. Overall, we see that investment/capital and consumption/capital responses are noticeably sensitive to the choice of \(\lambda\).
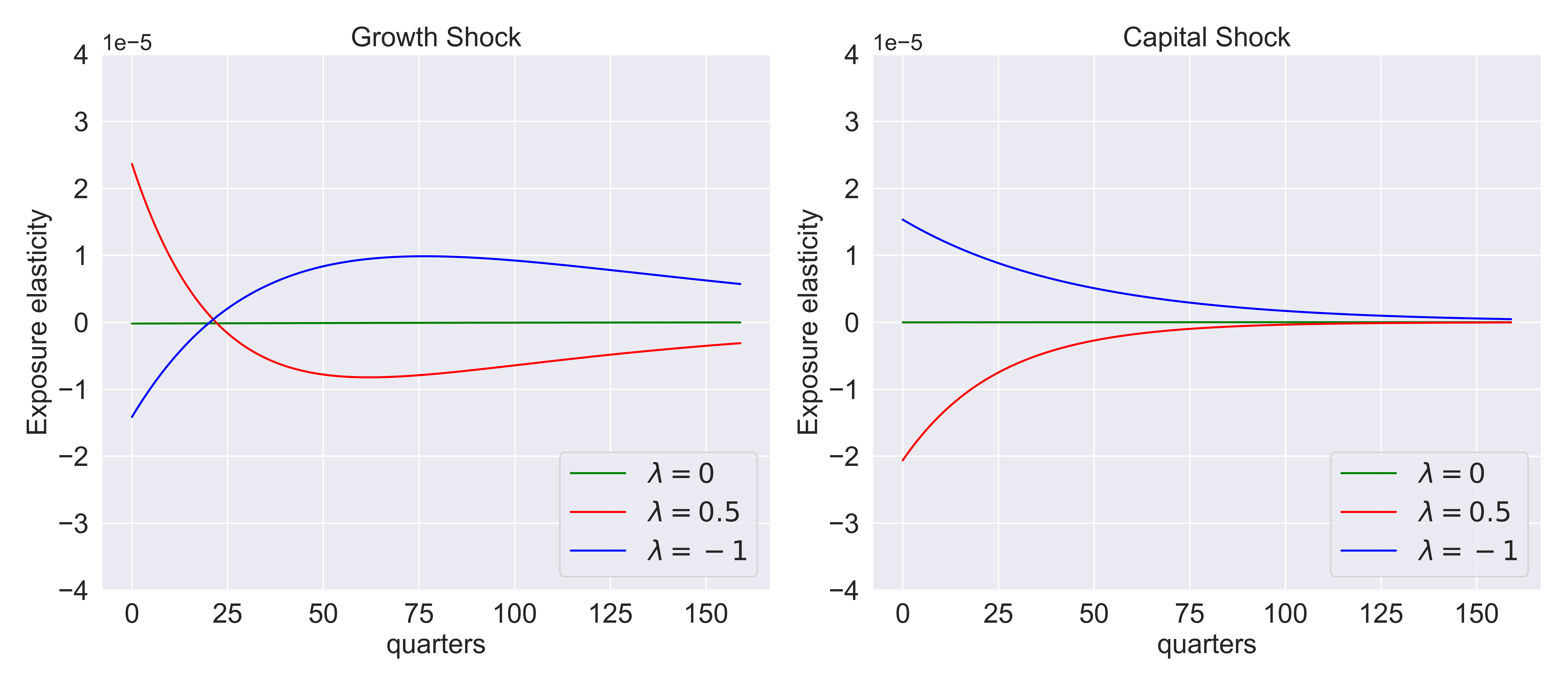
Fig. 8.6 Investment/capital exposure elasticities for the growth and capital shocks with different values of \(\lambda.\)#
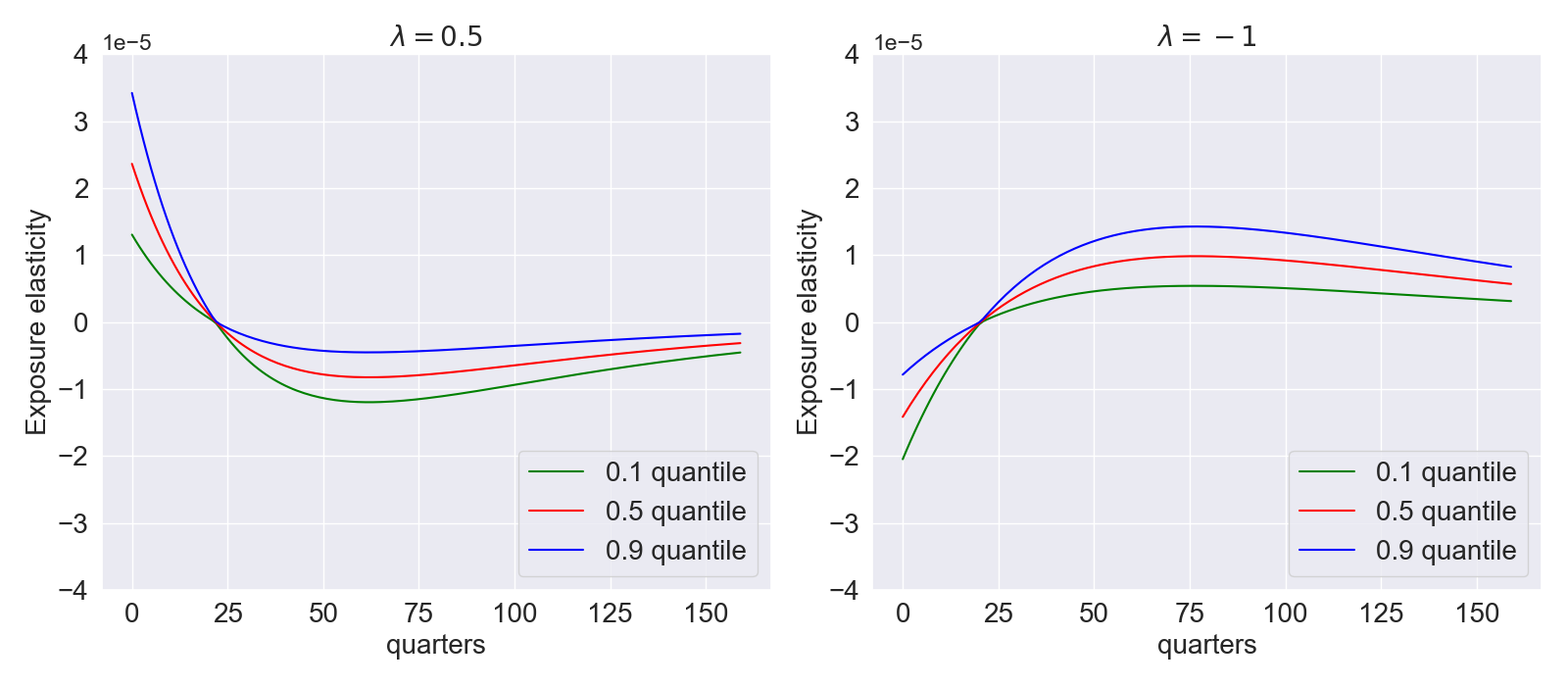
Fig. 8.7 Investment/capital exposure elasticities for the growth shock with different values of \(\lambda\) and elasticity quantiles.#
We next consider the shock price elasticities for the growth shock. Fig. 8.8 reports the elasticities for three values of \(\gamma\) and \(\lambda = 0\). Recall that \(\gamma = 1\) is equivalent to investors having no concerns about robustness. Since \(\lambda=0,\) this figure repeats earlier results and is included here for comparison. As we noted in previous discussion, these elasticities increase in the value of \(\gamma\) ( increase in the concern about robustness) and become very flat for larger values of \(\gamma\) as the martingale component to the stochastic discount factor process comes to dominate. Fig. 8.9 considers the growth shock price elasticities when \(\lambda=.5\). These elasticities are similar to the ones reported for \(\lambda = 0\) in Fig. 8.8, although there is small drop in the magnitudes relative the \(\lambda = 0\) specifcation. Fig. 8.10 explores the same elasticities when \(\lambda = -1\). We now see a modest increase in the shock price elasticities relative to the two previous figures.
Fig. 8.8 Price elasticities for the growth shock for \(\lambda=0\) and different values of \(\gamma\).#
Fig. 8.9 Price elasticities for the growth shock for \(\lambda=0.5\) and different values of \(\gamma\).#
Fig. 8.10 Price elasticities for the growth shock for \(\lambda=-10\) and different values of \(\gamma\).#
Overall, we see that investment/capital and consumption/capital impulse responses are noticeably sensitive to the choice of \(\lambda\), which should be expected given the impact of this parameter on intertemporal substitution in preferences. In contrast, \(\lambda\) has a small impact on the shock price elasticities. These elasticities are, however, notably sensitive to the choice of \(\gamma,\) which is consistent with recursive utility construction of uncertainty aversion.
[Pollak, 1970] introduced a version of external habit persistence in consumer demand function. The stock \(H_t\) enters preferences as a societal or external input and not recognizable as an individual input in the current time period. Thus there is an externality induced by this specification of preferences. [Abel, 1990] and [Campbell and Cochrane, 1999] explore implications along with many subsequent papers explore asset pricing with external habit persistence. Much of the latter literature abstracts from production, but there are exceptions. See for instance, [Lettau and Uhlig, 2000]. The equilibrium solution with external habit persistence deviates from the planner problem in that the co-state for \(H_t\) is now zero and the co-state equation is omitted from the equations to be solved and approximated.
8.7.6. External habits model#
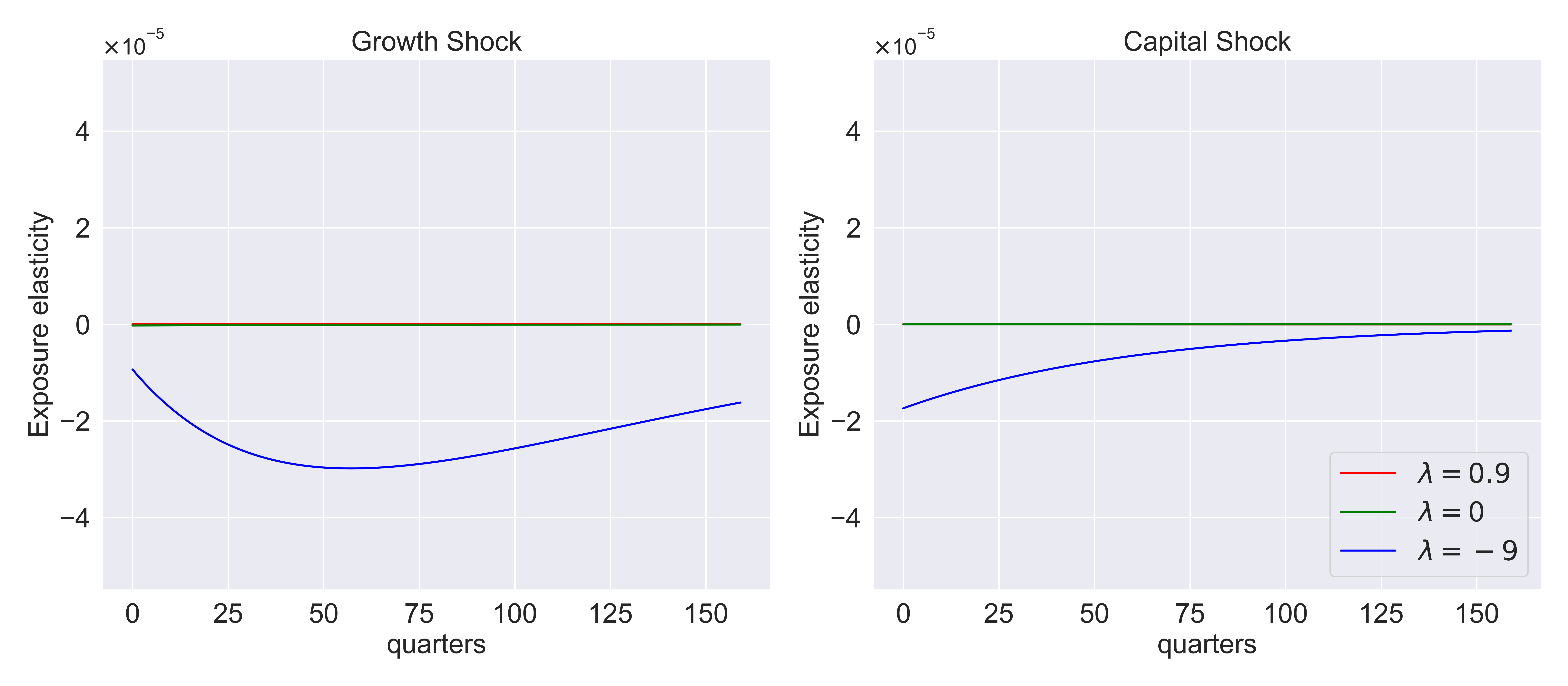
Fig. 8.11 Investment/capital exposure elasticities for the growth and capital shocks with different values of \(\lambda.\)#
Please note that the axes in the left panel on the graph below are scaled 0.01 times relative to the right panel.
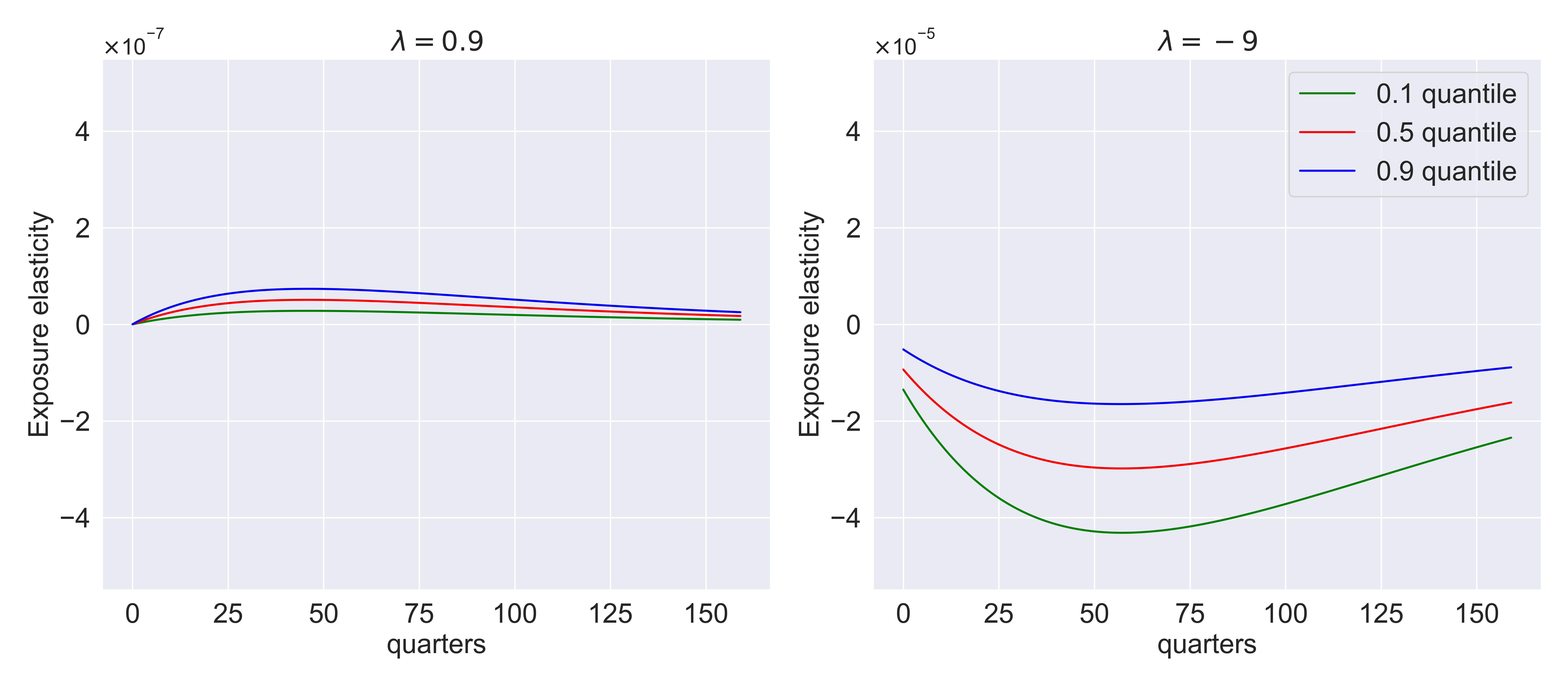
Fig. 8.12 Investment/capital exposure elasticities for the growth shock with different values of \(\lambda\) and elasticity quantiles.#
8.8. Solving models#
In this section, we briefly describe one way to extend the approach that builds directly on previous second-order approaches of [Kim et al., 2008], [Schmitt-Grohé and Uribe, 2004], and [Lombardo and Uhlig, 2018]. While such methods should not be viewed as being generically applicable to nonlinear stochastic equilibrium models, we find them useful pedagogically and often as at least initial steps to understanding models that are arguably “smooth.” See [Pohl et al., 2018] for a careful study of nonlinearity in asset pricing models with recursive utility.[7]
We implement these methods for second-order approximation using the following steps.
Solve for \({\sf q}=0\) deterministic model.
Take as given first and second-order approximate solutions for \({\widehat C}_t - {\widehat G}_t\) and \({\widehat G}_{t+\epsilon} - {\widehat G}_t.\). Solve for the approximate solutions for \({\widehat V}_t - {\widehat G}_t,\) \({\widehat V}_{t+\epsilon} - {\widehat R}_t\) and \(N_{t+\epsilon}.\)
Compute the first-order expansion and solve the resulting equations following the previous literature for \(D_t,\) \({\widehat C}_t - {\widehat G}_t,\) and \({\widehat G}_{t+\epsilon} - {\widehat G}_t.\) When constructing these equations, use expectations computed using the probabilities induced by \(N_{t+\epsilon}^0\). Substitute the first-order approximation for \({\widehat R}_t - {\widehat G}_t.\)
Compute the second-order expansion and solve the resulting equations following the previous literature. Again use the expectations induced by \(N_{t+\epsilon}^0\). In addition, make another recursive utility adjustment expressed in terms the approximations of \({\widehat R}_t - {\widehat G}_t.\)
Return to step 2, and repeat until convergence.
Initialize this algorithm by solving the \(\gamma_o=1\) and \(\rho = 1,\) which can be solved without iteration.
See the Appendices that follow for more details and formulas to use in the solution method.
As a second approach we iterate over an \(N_{t+\epsilon}^*\) given by formula (8.30) approximation restricted to induce an alternative probability distribution Call the approximation \({\widetilde N}_{t+\epsilon}\) with an induced distribution for \(W_{t+\epsilon}\) that is normal with conditional mean \({\tilde \mu}_t\) and covariance matrix \({\widetilde \Sigma}\).
While we discussed the approximation for resource allocation problems with recursive utility, there is a direct extension of this approach to solve a general class stochastic equilibrium models by stacking a system of expectational-type equations expressed in part using the recursive utility stochastic discount factor that we derived. For resource allocation problems, we expressed the first-order conditions for the planner in utility units, which simplified some formulas. Equilibrium models not derived from a planner’s problems typically use stochastic discount factors expressed in consumption units when representing investment choices. The approximation methods described in this chapter have a direct extension to such models.
8.9. Appendix A: Solving the planner’s problem#
Write the system of interest, including the state equations (8.31), the consumption equation and static constraint (8.32), the first-order conditions (8.33), and the co-state evolution (8.34) as:
where
Here, for computational purposes, we use that \({\widehat C}_t - {\widehat V}_t = \left({\widehat C}_t - {\widehat G}_t\right) - \left({\widehat V}_t - {\widehat G}_t\right)\). We solve for \( {\widehat C}_t - {\widehat G}_t, D_t, MX_t\) as a function of \(X_t\). The objects: \({\widehat C} - {\widehat G}, D\) and \(MX\) are sometimes referred to as jump variables since we not impose initial conditions for these variables as part of a solution.
Our solution will entail an iteration. We will impose a specification for \(Q^1, Q^2, \) and \(N\) and find an approximate solution for the dynamical system. Then given this solution, we will compute a new implied solution for \(Q^1, Q^2,\) and \(N\). We then iterate this until we achieve numerical convergence. We use second-order approximations for both steps.
8.9.1. Some steady state calculations#
Observe from the recursive utility updating that:
In the steady state we view this as two equations in three variables: \({\widehat V}_t^0 - {\widehat G}_t^0 , {\widehat R}_t^0 - {\widehat G}_t^0\) and \({\widehat G}_{t+1}^0 - {\widehat G}_t^0\), each of which we assume is time invariant.
We construct
and
in the steady state, and use them to construct the remaining steady-state equations:
In this equation, \(H_{t+1}^0, L_t^0,\) and \(M_t^0\) are constructed from the formulas for \(H_{t+1}, L_t\) M_t$, defined previously, by setting the shock vector to zero and treating the relevant variables as time invariant.
8.9.2. \(Q\) and \(P\) derivatives#
For the order one, write
To compute this contribution, we equation (8.19) to write
We then construct
To compute \({\widehat V}_t - {\widehat G}_t \), we rewrite (8.23) as:
and solve this equation forward by first computing the \(\gamma_o=1\) answer and then adjusting this answer for \(\gamma_o > 1\) analogous to the approach described in Remark 8.5.
For the order two approximation,
Express:
It follows from (8.29) that
which we solve this equation forward under the \(N^0\) implied change in probability measure. Form:
The \(P\) approximations use some of these same computations where
8.9.3. \(N\) derivatives#
Form:
It may be directly verified that \(N_{t+1}^1\) and \( N_{t+1}^2\) have conditional expectations equal to zero. Express
In producing these representations, we use that have conditional \({\widehat V}_{t+1}^2 - {\widehat R}_{t}^2\) and \( {\widehat V}_{t+1}^2 - {\widehat R}_{t}^2\) have mean zero under the conditional probability distribution induced by \(N_{t+1}^0.\)
8.10. Appendix B: Approximation formulas (approach one)#
Consider the equation:
not including the state evolution equations.
8.10.1. Order zero#
The order zero approximation of the product: \( N_{t+1} Q_{t} H_{t+1} + P_t L_{t} - M_0\) is:
Thus the order zero approximate equation is:
since \( N_{t+1}^0 \) has conditional expectation equal to one. We add to this subsystem the \({\sf q} = 0\) state dynamic equation inclusive of jump variables, and we compute a stable steady state solution.
8.10.2. Order one#
The order one approximation of the product: \( Q_t N_{t+1} H_{t+1}+ P_t L_{t} - M_t \) is:
Thus the order one approximate equation is:
where we used the implication that \( {\mathbb E} \left( N_{t+1}^1 \mid {\mathfrak A}_t \right) = 0.\)
8.10.3. Order two#
The order two approximation of the product: \( Q_t N_{t+1} H_{t+1} + P_t L_{t} - M_t \) is:
The terms \( Q_t^0 N_{t+1}^2H_{t+1}^0\) and \(2 N_{t+1}^1 Q_{t}^1 H_{t+1}^0\) have conditional expectation equal to zero. Thus the approximating equation is:
To elaborate on the contributions in the second line, express \( H_{t+1}^1 \) as
Then
The formula for the first of these terms follows from (8.39) and (8.40), along with fact the third central moments of normals are zero.
We add to this second-order subsystem, the second-order approximation of the state dynamics inclusive of the jump variables. We substitute in the solution for the first-order approximation for the jump variables into both the first and second-order approximate state dynamics. In solving the second-order jump variable adjustment we use expectations induced by \( N_{t+1}^0 \) zero throughout under which \(W_{t+1} \) is conditionally normally distributed with mean \( \mu^0 \) and covariance \( I \).
8.11. Appendix C: Approximation formulas (approach two)#
In this approach we use the same order zero approximation. For the order one approximation, we use the formula (8.30) for \({\widetilde N}_{t+1},\) which approximates \(N_{t+1}^*,\) in conjunction with:
From formula (8.39), it follows that under the \({\widetilde N}_{t+1},\) induced change in probability, \(W_{t+1}\) is normally distributed with conditional mean
and conditional precision:
For the order two approximation, we use:
8.12. Appendix D: Parameter values#
To facilitate a comparison to a global solution method, we write down a discrete-time approximation to a continuous time version of such an economy. (See Section 4.4 of [Hansen et al., 2024] for a continuous-time benchmark model that our discrete-time system approximates. Note that we convert the annual parameters in that paper to quarterly time.) The parameter settings are:
\(\delta\) |
\(\iota_k\) |
\(\zeta\) |
\(\nu_k\) |
\(\nu_1\) |
\(\nu_2\) |
\(\mu_2\) |
|---|---|---|---|---|---|---|
0.025 |
0.01 |
32 |
0.01 |
0.014 |
0.0485 |
\(6.3 \times 10^{-6}\) |
The numbers for \(\eta_k, \phi, \beta_1,\) \(\sigma_k\) and \(\sigma_1\) are such that, when multiplied by stochastic volatility, they match the parameters from [Hansen and Sargent, 2021]. In particular, the constant \(Z^2\) which scales our \(\sigma_k\) to match is \(7.6\times10^{-6},\) which is the 67th percentile of our \(Z^2\) distribution. While [Hansen and Sargent, 2021] use a lower triangular representation for the two-by-two right block of
we use an observationally equivalent upper triangular representation for most of the results. Finally, the numbers for \(\beta_2\) and \(\sigma_2\) come from [Schorfheide et al., 2018], but they are adjusted for approximation purposes as described in Appendix A [Hansen et al., 2024]. In both cases, we use the medians of their econometric evidence as input into our analysis.
For the extension to the habit persistence model in Section 8.7.5, we use a habit persistence of \(\nu_h = 0.025\).
