11. Risk, Ambiguity, and Misspecification[1]

\(\newcommand{\eqdef}{\stackrel{\text{def}}{=}}\)

---

“Uncertainty must be taken in a sense radically distinct from the familiar notion of risk, from which it has never been properly separated…. and there are far-reaching and crucial differences in the bearings of the phenomena depending on which of the two is really present and operating.” [Knight, 1921]

11.1. Introduction

Likelihood functions are probability distributions conditioned on parameters; prior probability distributions describe a decision maker’s subjective belief about those parameters.[2] By distinguishing roles played by likelihood functions and subjective priors over their parameters, this chapter brings some recent contributions to decision theory into contact with statistics and econometrics in ways that can address practical econometric concerns about model misspecifications and choices of prior probabilities.

We combine ideas from control theories that construct decision rules that are robust to a class of model misspecifications with axiomatic decision theories invented by economic theorists. Such decision theories originated with axiomatic formulations by von Neumann and Morgenstern, Savage, and Wald ([Wald, 1947, Wald, 1949, Wald, 1950], [Savage, 1954]). Ellsberg ([Ellsberg, 1961]) pointed out that Savage’s framework seems to include nothing that could be called “uncertainty” as distinct from “risk”. Theorists after Ellsberg constructed coherent systems of axioms that embrace a notion of ambiguity aversion. However, most recent axiomatic formulations of decision making under uncertainty in economics are not cast explicitly in terms of likelihood functions and prior distributions over parameters.

This chapter reinterprets objects that appear in some of those axiomatic foundations of decision theories in ways useful to an econometrician. We do this by showing how to use an axiomatic structure to express ambiguity about a prior over a family of statistical models, on the one hand, along with concerns about misspecifications of those models, on the other hand.

Although they proceeded differently than we do here, [Chamberlain, 2020], [Cerreia-Vioglio et al., 2013], and [Denti and Pomatto, 2022] studied related issues. [Chamberlain, 2020] emphasized that likelihoods and priors are both vulnerable to potential misspecifications. He focused on uncertainty about predictive distributions constructed by integrating likelihoods with respect to priors. In contrast to Chamberlain, we formulate a decision theory that distinguishes uncertainties about priors from uncertainties about likelihoods. [Cerreia-Vioglio et al., 2013] (section 4.2) provided a rationalization of the smooth ambiguity preferences proposed by [Klibanoff et al., 2005] that includes likelihoods and priors as components. [Denti and Pomatto, 2022] extended this approach by using an axiomatic revealed preference approach to deduce a parameterization of a likelihood function. However, neither [Cerreia-Vioglio et al., 2013] nor [Denti and Pomatto, 2022] sharply distinguished prior uncertainty from concerns about misspecifications of likelihood functions. We want to do that. We formulate concerns about statistical model misspecifications as uncertainty about likelihoods.

More specifically, we align definitions of statistical models, uncertainty, and ambiguity with ideas from decision theories that build on [Anscombe and Aumann, 1963]’s way of representing subjective and objective uncertainties. In particular, we connect our analysis to econometrics and robust control theory by using Anscombe-Aumann states as parameters that index alternative statistical models of random variables that affect outcomes that a decision maker cares about. By modifying aspects of [Gilboa et al., 2010], [Cerreia-Vioglio et al., 2013], and [Denti and Pomatto, 2022], we show how to use variational preferences to represent uncertainty about priors and also concerns about statistical model misspecifications.

Discrepancies between two probability distributions occur throughout our analysis. This fact opens possible connections between our framework and some models in “behavioral” economics and finance that assume that decision makers inside their models have expected utility preferences in which an agent’s subjective probability – typically a predictive density – differs systematically from the predictive density that the model user assumes governs the data.[3] Other “behavioral” models focus on putative differences among agents’ degrees of confidence in their views of the world. Our framework implies that the form taken by a “lack of confidence” should depend on the probabilistic concept about which a decision maker is uncertain. Preference structures that we describe in this chapter allow us to formalize different amounts of “confidence” about details of specifications of particular statistical models, on one hand, and about subjective probabilities to attach to alternative statistical models, on the other hand. Our representations of preferences provide ways to characterize degrees of confidence in terms of statistical discrepancies between alternative probability distributions.[4]

11.2. Background motivation

We are sometimes told that we live in a “data rich” environment. Nevertheless, data are often not “rich” along all of the dimensions that we care about for decision making. Furthermore, data don’t “speak for themselves”. To get them to say something, we have to posit a statistical model. For all the hype, the types of statistical learning we actually do is infer parameters of a family of statistical models. Doubts about what existing evidence has taught them about some important dimensions has led some scientists to think about what they call “deep uncertainties.” For example, in a recent paper we read:

“The economic consequences of many of the complex risks associated with climate change cannot, however, currently be quantified. … these unquantified, poorly understood and often deeply uncertain risks can and should be included in economic evaluations and decision-making processes.” [Rising et al., 2022]

In this chapter, we formulate “deep uncertainties” as lacks of confidence in how we represent probabilities of events and outcomes that are pertinent for designing tax, benefit, and regulatory policies. We do this by confessing ambiguities about probabilities, though necessarily in a restrained way.

In our experience as macroeconomists, model uncertainties aren’t taken seriously enough, too often being dismissed as being of “second-order”, whatever that means in various contexts. In policy making settings, there is a sometimes a misplaced wisdom that acknowledging uncertainty should tilt decisions toward passivity. But other times and places, one senses that the model uncertainty emboldens pretense:

“Even if true scientists should recognize the limits of studying human behavior, as long as the public has expectations, there will be people who pretend or believe that they can do more to meet popular demand than what is really in their power.” [Hayek, 1989]

As economists, part of our job is to delineate tradeoffs. Explicit incorporation of precise notions of uncertainty allows us to explore two tradeoffs pertinent to decision making. Difficult tradeoffs emerge when we consider implications from multiple statistical models and alternative parameter configurations. Thus, when making decisions, how much weight should we assign to best “guesses” in the face of our model specification doubts, versus possibly bad outcomes that our doubts unleash? Focusing exclusively on best guesses can lead us naively to ignore adverse possibilities worth considering. Focusing exclusively on worrisome bad outcomes can lead to extreme policies that perform poorly in more normal outcomes. Such considerations induce us to formalize tradeoffs in terms of explicit expressions of aversions to uncertainty.

There are also intertemporal tradeoffs: should we act now, or should we wait until we will have learned more? While waiting is tempting, it can also be so much more costly that it becomes prudent to take at least some actions now even though we anticipate knowing more later.

11.2.1. Aims

In this chapter we allow for uncertainties that include

• risks: unknown outcomes with known probabilities;

• ambiguities: unknown weights to assign to alternative probability models;

• misspecifications: unknown ways in which a model provides flawed probabilisties;

We will focus on formulations that are tractable and enlightening.

11.3. Decision theory overview

Decision theory under uncertainty provides alternative axiomatic formulations of “rationality.” As there are multiple axiomatic formulations of decision making under uncertainty, it is perhaps best to replace the term “rational” with “prudent.” While these axiomatic formulations are of intellectual and substantive interest, in this chapter we will focus on the implied representations. This approach remains interesting because we have sympathy for Savage’s own perspective on his elegant axiomatic formulation:

Indeed the axioms have served their only function in justifying the existential parts of Theorems 1 and 3; in further exploitation of the theory, …, the axioms themselves can end, in my experience, and should be forgotten.” [Savage, 1952]

11.3.1. Approach

In this chapter we will exploit modifications of Savage-style axiomatic formulations from decision theory under uncertainty, to investigate notions of uncertainty beyond risk. The overall aim is to make contact with applied challenges in economics and other disciplines. We will start with the basics of statistical decision theory and then proceed to explore extensions that distinguish concerns about potential misspecifications of likelihoods from concerns about the misspecification of priors. This opens the door to better ways for conducting uncertainty quantification for dynamic, stochastic economic models used for private sector planning and governmental policy assessment. It is achieved by providing tractable and revealing methods for exploring sensitivity to subjective uncertainties, including potential model misspecification and ambiguity across models. This will allow us to systematically:

• assess the impact of uncertainty on prudent decision or policy outcomes;

• isolate the forms of uncertainty that are most consequential for these outcomes.

To make the methods tractable and revealing we will utilize tools from probability and statistics to limit the type and amount of uncertainty that is entertained. As inputs, the resulting representations of objectives for decision making will require a specification of aversion to or dislike of uncertainty about probabilities over future events.

11.3.2. Anscombe-Aumann (AA)

[Anscombe and Aumann, 1963] provided a different way to justify Savage’s representation of decision making in the presence of subjective uncertainty. They feature prominently the distinction between a “horse race” and a “roulette wheel”. They rationalize preferences over acts, where an act maps states into lotteries over prizes. The latter is the counterpart to a roulette wheel. Probability assignments over states then become the subjective input and the counterpart to the “horse race.”

While [Anscombe and Aumann, 1963] used this formulation to extend the von Neumann-Morgenstern expected utility with known probabilities to decisions problems where subjective probabilities also play a central role as in Savage’s approach. While [Anscombe and Aumann, 1963] provides an alternative derivation of subjective expected utility, many subsequent contributions used the Anscombe-Aumann framework to extend the analysis to incorporate forms of ambiguity aversion. Prominent examples include [Gilboa and Schmeidler, 1989] and [Maccheroni et al., 2006]. In what follows we provide a statistical slant to such analyses.

11.3.3. Basic setup

Consider a parameterized model of a random vector with realization \(x\):

\[\ell(x \mid \theta) d \tau(x) \]

where

\[\int_{\mathcal X} \ell(x \mid \theta) d \tau(x) = 1,\]

\(\theta \in \Theta\) and \(\Theta\) is a parameter space, and \(\mathcal X\) is the space of possible realizations of \(x\). We refer to \(\ell\) as a likelihood and the probability implied by each \(\theta\) as a “structured” probability model.

Denote by \(\pi\) a prior distribution over \(\Theta.\) We will sometimes have reason to focus on a particular prior, \(\pi\) that we will call a baseline prior. We denote a prize rule by \(\gamma\) which maps \(\mathcal X\) into prizes. We define a decision rule, \(\delta,\) that can condition on observations or signals. To elaborate further, partition \(x = (w, z)\) where the decision rule can depend on \(z,\) and the prize rule on the entire \(x\) vector. A probability distribution over the \(w\)’s reflects random outcomes realized after a decision has been made. For instance, in an intertemporal context, \(w\) may reflect future shocks. Thus decisions may have further repercussions for prizes beyond \(z\):

\[\gamma_\delta(x) = \Psi[ \delta(z), x ].\]

Since the decision rule can depend on \(z\) , ex post learning is entertained. Decision rules are restricted to be in a set \(\Delta\) and imply restrictions for prize rules:

\[\Gamma(\Delta) \eqdef \{ \gamma_\delta : \delta \in \Delta \}.\]

The preferences over prize rules imply a ranking over decision rules, the \(\delta\)’s, in \(\Delta\). While we are featuring the impact of a decision rule on a prize rule, we may extend the analysis to allow \(\delta\) to influence \(\ell\) as happens when we entertain experimentation.

Risk is assessed using expected utility with a utility function \({U}\). We compute the expected utility for prize rules as a function of \(\theta\) as:

\[{\overline {U}}(\gamma \mid \theta) = \int_{\mathcal X} {U}[\gamma(x), \theta] \ell(x \mid \theta) d \tau(x) .\]

Following a language from statistical decision theory, we call \({\overline {U}}(\gamma \mid \theta)\) the risk function for a given prize rule when viewed as a function of \(\theta.\)[5]

We allow the utility function to depend on the unknown parameter \(\theta,\) as is common in statistical decision problems. Arguably, such a formulation is short hand for a more primitive specification in which the parameter has ramifications for a future prize.

11.3.4. A simple statistical application

As an illustration, we consider a model selection problem. Suppose \(\Theta = \{\theta_1, \theta_2\},\) and that the decision maker can use the entire underlying random vector. Thus, we make no distinction between \(\gamma\) and \(\delta\) and no distinctions between \(x\) and \(z\).

The decision rule, \(\delta = \gamma\) is a mapping from \(\mathcal Z\) to \([0,1]\) where \(\delta(z) = 1\) means that the decision maker selects model \(\theta_1\) and \(\delta(z) = 0\) means that the decision maker selects model \(\theta_2.\)
We allow for intermediate values between zero and one, which can be interpreted as randomization. These intermediate choices will end up not being of particular interest for this example.

The utility function for assessing risk is:

\[\begin{split} {U}(\delta, \theta_1) & = \upsilon_1 \delta \cr {U}(\delta, \theta_2) & = \upsilon_2 (1 - \delta) \end{split} \]

where \(\upsilon_1,\) and \(\upsilon_2\) are positive utility parameters.

A class of decision rules, called threshold rules, will be of particular interest. Partition \(\mathcal Z\) into two sets:

\[\mathcal Z = \mathcal Z_1 \cup \mathcal Z_2,\]

where the intersection of \(\mathcal Z_1\) and \(\mathcal Z_2\) is empty. A threshold rule has the form:

\[\delta(z) = \left\{ \begin{matrix} 1 & \textrm{ if } z \in \mathcal Z_1 \cr 0 & \textrm{ if } z \in \mathcal Z_2 .\end{matrix} \right.\]

For a threshold rule, the conditional expected utility is

\[\begin{split} {\overline {U}}(\gamma \mid \theta_1)& = \upsilon_1 \int_{\mathcal Z_1} \ell(z \mid \theta_1) d \tau(z) \cr {\overline {U}}(\gamma \mid \theta_2) & = \upsilon_2 \int_{\mathcal Z_2} \ell(z \mid \theta_2) d\tau(z). \end{split}\]

Suppose that the utility weights \(\upsilon_1\) and \(\upsilon_2\) are both one. Under this threshold decision rule, \(1 - {\overline {U}}(\gamma \mid \theta_1)\) is the probability of making a mistake when model \(\theta_1\) generates the data, and \(1 - {\overline {U}}(\gamma \mid \theta_2)\) is the probability of making a mistake if model \(\theta_2\) generates the data. In statistics, the first of these is called a type I error and type II depending assuming we consider \(\theta_1\) to be the “null model” and \(\theta_2\) to be the alternative. The utility weights determine relative importance to the decision maker of making a correct identification of the model.

11.4. Subjective expected utility

Order preferences over \(\gamma\) and hence \(\delta\)

\[\int_\Theta \left[ \int_{\mathcal X} {U}[\gamma(x), \theta] \ell(x | \theta) d \tau(x) \right] d\pi(\theta) = \int_\Theta {\overline {U}} (\gamma \mid \theta) d\pi(\theta) \]

for a specific \(\pi.\) This representation is supported by Savage and Anscombe-Aumann axioms, but imposes full confidence with no potential misspecification of the priors or the likelihood.

We use these preference for a decision problem where prize rules are restricted to be in the set \(\Gamma(\Delta)\):

Problem 11.1

(11.1)\[\max_{\gamma \in \Gamma(\Delta)} \int_\Theta \left(\int_{\mathcal X} {U}[\gamma(x), \theta] \ell(x | \theta) d \tau(x) \right) d\pi(\theta).\]

Recall that partitioning of \(x = (w, z)\) where the decision rule can only depend on \(z\) and the prize rule on the entire \(x\) vector. Factor \(\ell(\cdot \mid \theta)\) and \(\tau\) as:

(11.2)\[\begin{split} d \tau(x) & = d \tau_2(w) d\tau_1(z) \cr \ell(x \mid \theta) & = \ell_2(w \mid z, \theta) \ell_1(z \mid \theta) \end{split}\]

These factorizations in (11.2) allow us to write the objective as:

\[\int_\Theta \left[\int_{\mathcal Z} \left(\int_{\mathcal W} {U}[\gamma(x), \theta] \ell_2(w \mid z, \theta) d \tau_2(w )\right) \ell_1(z \mid \theta) d \tau_1(z)\right] d\pi(\theta).\]

To solve problem (11.1), it is convenient to exchange the orders of integration in the objective:

\[\int_{\mathcal Z}\left[ \int_{\Theta}\left( \int_{\mathcal W} {U}[\gamma(x), \theta] \ell_2(w \mid z, \theta) d \tau_2(w) \right) \ell_1(z \mid \theta) d\pi(\theta) \right] d \tau_1(z) \]

Notice that even if the utility function \({U}\) does not depend on \(\theta\), this dependence may emerge after we integrate over \({\mathcal W}\) because of the dependence of \(\ell_2(\cdot \mid \theta)\) on the unknown parameter.

As \(\delta\) only depends on \(z\) and the objective is additively separable in \(z\), we may solve a conditional problem: using the objective:

\[{\widetilde {U}}[\delta(z)] \eqdef \int_{\Theta}\left( \int_{\mathcal W} {U}\left(\Psi[\delta(z), w, z], \theta \right) \ell_2(w \mid z, \theta) d \tau_2(w) \right) \ell_1(z \mid \theta) d\pi(\theta) \]

for each value of \(z\) provided that the restrictions imposed on \(\delta\) by the construction of the set of decision rules \(\Delta\) are separable in \(z\). That is, provided that we can write:

(11.3)\[\Delta = \left\{ \delta: \delta(z) \in \Delta(z) \textrm{ for all } z \in \mathcal Z \right\} \]

for given constraint sets \(\Delta(z),\) we may solve

Problem 11.2

(11.4)\[\max_{\delta(z) \in \Delta(z)} \widetilde {U}[\delta(z)]\]

Finally, notice that

\[d{\bar \pi}(\theta \mid z) \eqdef \left[\frac { \ell_1(z \mid \theta)} { \int_\Theta \ell_1(z \mid \theta) d\pi(\theta)} \right] d\pi(\theta)\]

is the Bayesian posterior distribution for \(\theta.\) Equivalently, we may solve the conditional Bayesian problem:

Problem 11.3

(11.5)\[\max_{\delta(z) \in \Delta(z)} \int_\Theta \left(\int_{\mathcal W} {U}[\Psi(\delta(z), w, z), \theta] \ell_2( w \mid z, \theta) d \tau_2(w) \right) d{\bar \pi} (\theta \mid z),\]

since in forming the objective of conditional problem, (11.5), we divided the objective for the conditional problem, (11.4) by a function of \(z\) alone.

For illustration purposes, consider the example given in Section A simple statistical application. In this example, \(x = z\) and there is no \(w\) contribution. Impose prior probabilities, \( \pi(\theta_1),\) and \( \pi(\theta_2) = 1 - \pi(\theta_1)\) on the two models. Compute the Bayesian posterior probabilities for each value of \(\theta,\)

\[\begin{split} \bar \pi (\theta_1 \mid z)& = \frac { \ell(z \mid \theta_1) \pi(\theta_1)} { \ell(z \mid \theta_1)\pi(\theta_1) + \ell(z \mid \theta_2) \pi(\theta_2) } \cr \bar \pi (\theta_2 \mid z)& = \frac { \ell(z \mid \theta_2) \pi(\theta_2)} { \ell(z \mid \theta_1)\pi(\theta_1) + \ell(z \mid \theta_2) \pi(\theta_2) } \end{split}\]

Consider the conditional problem. If the decision maker chooses model one, then the conditional expected utility is \( \upsilon_1 \bar \pi (\theta_1 \mid z) \) and similarly for choosing model two. Thus the Bayesian decision maker computes:

\[\max \left\{ \upsilon_1 \bar \pi (\theta_1 \mid z), \upsilon_2 \bar \pi(\theta_2 \mid z) \right\}\]

and chooses a model in accordance to this maximization. This maximization is equivalent to

\[\max \left\{ \upsilon_1 \pi (\theta_1) \ell(z \mid \theta_1) , \upsilon_2 \pi(\theta_2 )\ell(z \mid \theta_2) \right\}\]

expressed in terms of the prior, likelihood, and utility contributions. Taking logarithms and rearranging, we see that model \(\theta_1\) is selected if

(11.6)\[\log \ell(z \mid \theta_1) - \log \ell(z \mid \theta_2) \ge \log \upsilon_2 - \log \upsilon_1 + \log \pi(\theta_2) - \log \pi(\theta_1)\]

If the right side of this inequality is zero, say because prior probabilities are the same across models and utility weights are also the same, then the decision rule says to maximize the log likelihood. More generally both prior weights and utility weights come into play.

Notice that this decision rule is a threshold rule where we use the posterior probabilities to partition the \(\mathcal Z\) space. The subset \(\mathcal Z_1\) contains all \(z\) such that inequality (11.6) is satisfied with a weak inequality. We arbitrarily include the indifference values in \(\mathcal Z\).

The Bayesian solution to the decision problem is posed assuming full confidence in a subjective prior distribution. In many problems, including ones with multiple sources of uncertainty, such confidence may well not be warranted. Such a concern might well have been the motivation behind Savage’s remark:

… if I knew of any good way to make a mathematical model of these phenomena [vagueness and indecision], I would adopt it, but I despair of finding one. One of the consequences of vagueness is that we are able to elicit precise probabilities by self-interrogation in some situations but not in others.

Personal communication from L. J. Savage to Karl Popper in 1957

11.5. An extreme response

Suppose we go to the other extreme and avoid imposing a prior altogether. Compare two prize rules, \(\gamma_1\) and \(\gamma_2\), by computing the conditional (on \(\theta\)) expected utilities, \({\overline {U}} [\gamma_1, \theta]\) and \({\overline {U}} [\gamma_2, \theta]\) for each \(\theta \in \Theta\). Then \(\gamma_2\) is preferred to \(\gamma_1\) if the conditional expected utility of the former exceeds that of the latter for all \(\theta \in \Theta\). This, however, only implies a partial ordering among prize rules. Many such rules cannot be ranked. This partial ordering gives rise to a construct called admissibility, where an admissible \(\delta \in \Delta\) cannot be dominated in the sense of this partial order.

11.5.1. Constructing admissible decision rules

One way to construct an admissible decision rule is to impose a prior and solve the resulting Bayesian decision problem. We give two situations in which this result necessarily applies, but there are other settings where this result is known to hold.

Proposition 11.1

If an ex ante Bayesian decision problem, (11.1), has a unique solution (except possibly on a set that has measure zero under \(\tau_2\)) , then this Bayesian solution is admissible.

Proof. Let \({\tilde \delta}\) be a decision rule that weakly dominates a Bayesian decision rule, \(\delta\), in the sense that

\[{\overline U} (\delta \mid \theta) \le {\overline U}( {\tilde \delta} \mid \theta)\]

for \(\theta \in \Theta.\) The \(\tilde \delta\) must also solve the ex ante Bayesian decision problem. Since the solution to the ex ante decision problem is unique, \({\tilde \delta} = \delta\).

Proposition 11.2

Suppose \(\Theta\) has a finite number of elements. If a prior distribution \(d\pi\) assigns positive probability to each element of \(\Theta,\) then a decision rule that solves the Bayesian decision problem (11.1) is admissible.

Proof. Let \({\tilde \delta}\) be a decision rule that weakly dominates a Bayesian decision rule, \(\delta\), in the sense that

(11.7)\[{\overline U} (\delta \mid \theta) \le {\overline U}( {\tilde \delta} \mid \theta)\]

for \(\theta \in \Theta.\) Suppose that the prior, \(d\pi,\) used in constructing the decision rule,\(\delta,\) assigns strictly positive probability to each value of \(\theta \in \Theta\). Use this prior to form expectations of both sides of inequality (11.7),

\[\int_\Theta {\overline U} (\delta \mid \theta) d\pi(\theta) \le \int_\Theta {\overline U}( \tilde \delta \mid \theta) d \pi(\theta) \]

But this latter inequality must hold with equality. Since each element of \(\Theta\) has strictly positive positive prior probability, inequality (11.7) must also hold with equality. Therefore, \(\delta\) must be admissible.

Remark 11.1

While we are primarily interested in the use of alternative subjective priors as a way to construct admissible decision rules, sufficient conditions have been derived under which we can find priors that give Bayesian justifications for all admissible decision rules. Such results come under the heading of Complete class theorems. See, for instance, [LeCam, 1955], [Ferguson, 1967], and [Brown, 1981].

11.5.2. A simple statistical application reconsidered

For illustration purposes, we again consider the model selection example. Consider a threshold decision rule of the form:

(11.8)\[\delta_{\sf r} (z) = \left\{ \begin{matrix} 1 & \log \ell(z \mid \theta_1) - \log \ell(z \mid \theta_2) \ge {\sf r} \cr 0 & \log \ell(z \mid \theta_1) - \log \ell(z \mid \theta_2) < {\sf r} \end{matrix} \right. \]

From formula (11.6), provided that we choose the prior probabilities to satisfy:

(11.9)\[\log \pi(\theta_2) - \log \pi(\theta_1) = {\sf r} + \log \upsilon_1 - \log \upsilon_2 , \]

threshold rule (11.8) solves a Bayesian decision problem. Thus the implicit prior for the threshold rule is:

\[\begin{split} \pi(\theta_1) &= \frac 1 { 1+ \exp \left( {\sf r} \right) \left( \frac {\upsilon_1} {\upsilon_2} \right)} \cr \cr \pi(\theta_2) & = \frac {\exp \left( {\sf r} \right) \left( \frac {\upsilon_1} {\upsilon_2} \right)} { 1+ \exp \left( {\sf r} \right) \left( \frac {\upsilon_1} {\upsilon_2} \right)}. \end{split} \]

To provide a complementary analysis, form:

\[y = \log \ell (z \mid \theta_1) - \log \ell (z \mid \theta_2), \]

and use the probability measure for \(z\) under model \(\theta_1\) to induce a corresponding probability measure for the scalar \(y\). Suppose this probability measure has a density \(f( \cdot \mid \theta_1) \) relative to Lebesgue measure. Observe that the counterpart density, \(f(\cdot \mid \theta_2)\) satisfies:

\[f(y \mid \theta_2) = \exp(-y) f(y \mid \theta_1)\]

For a decision rule, \(\delta_{\sf r}, \) with threshold \({\sf r},\) compute the two risks:

\[\begin{split} {\overline u}_1({\sf r}) \eqdef {\overline U}(\delta_{\sf r} \mid \theta_1) & = \upsilon_1 \int_{\sf r}^{+\infty} f(y \mid \theta_1) dy \cr {\overline u}_2({\sf r}) \eqdef {\overline U}(\delta_{\sf r} \mid \theta_2) & = \upsilon_2 \int_{-\infty}^{\sf r} \exp(-y) f(y \mid \theta_1) dy \end{split} \]

where we include the multiplication by \(\exp(-y)\) in the second row to change the computation using the model \(\theta_2\) probabilities.

Consider the two-dimensional curve of model risks, \(({\overline u}_1({\sf r}), {\overline u}_2({\sf r})),\) parametrized by the threshold \({\sf r}\). The slope of this curve at point corresponding to \({\sf r}\) is the ratio of the two derivatives with with respect to \({\sf r}\):

\[\frac { d {\overline u}_2({\sf r})/dr }{d {\overline u}_1({\sf r})/dr} = - \left( \frac {\upsilon_2}{\upsilon_1} \right) \exp(-{\sf r})\]

The second order derivative is

\[- \frac {\upsilon_2 \exp(-{\sf r})} {(\upsilon_1)^2f({\sf r})} < 0, \]

and hence the curve is concave.

Using prior probabilities to weight the two risks gives:

\[\pi(\theta_1) {\overline u}_1({\sf r}) + \pi(\theta_2) {\overline u}_2({\sf r})\]

Maximizing this objective by choice of a threshold \({\sf r}\) gives the first-order conditions:

\[- \pi(\theta_1) \upsilon_1 f({\sf r}) + \pi(\theta_2) \upsilon_2 \exp(-{\sf r})f({\sf r}) = 0,\]

implying that

\[\left( \frac {\upsilon_2}{\upsilon_1} \right) \exp(-{\sf r}) = \frac {\pi(\theta_1)}{\pi(\theta_2)}\]

As expected, this agrees with (11.9). Thus the negative of the slope of the curve reveals the ratio of probabilities that would justify a Bayesian solution given a threshold \({\sf r}\).

We illustrate this computation in Figures Fig. 11.1 and Fig. 11.2. Both figures report the upper boundary of the set of. feasible risks for alternative decision rules. The risks along the boundary are attainable with admissible decision rules. The utility weights, \(\upsilon_1\) and \(\upsilon_2\) are both set to one in Figure Fig. 11.1, and \(\upsilon_2\) is to \(.5\) in Figure Fig. 11.2. Thus ,the upper envelop of risks is flatter in Figure Fig. 11.2 than in Figure Fig. 11.1. The flatter curve implies prior probabilities that are close to being the same.

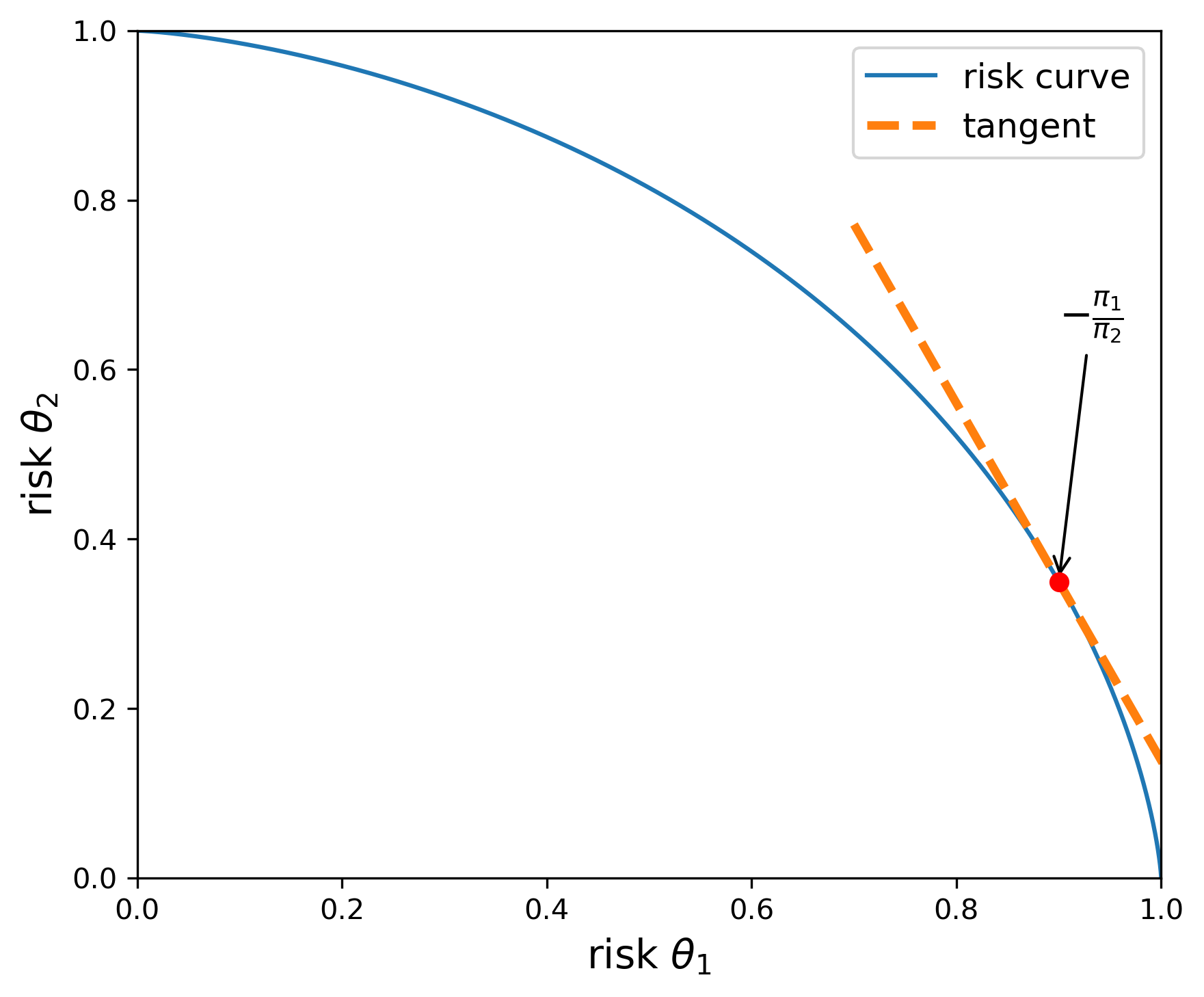
Fig. 11.1 The blue curve gives the upper boundary of the feasible set of risks. The utility function parameters are given by \(\upsilon_1=\upsilon_2=1.\) When \({\overline u}_{\sf r}(\theta_1) = .9\), the implied prior is given by \(\pi(\theta_1) =.68\) and \(\pi(\theta_2)=.32,\) as implied by the slope of the tangent line.

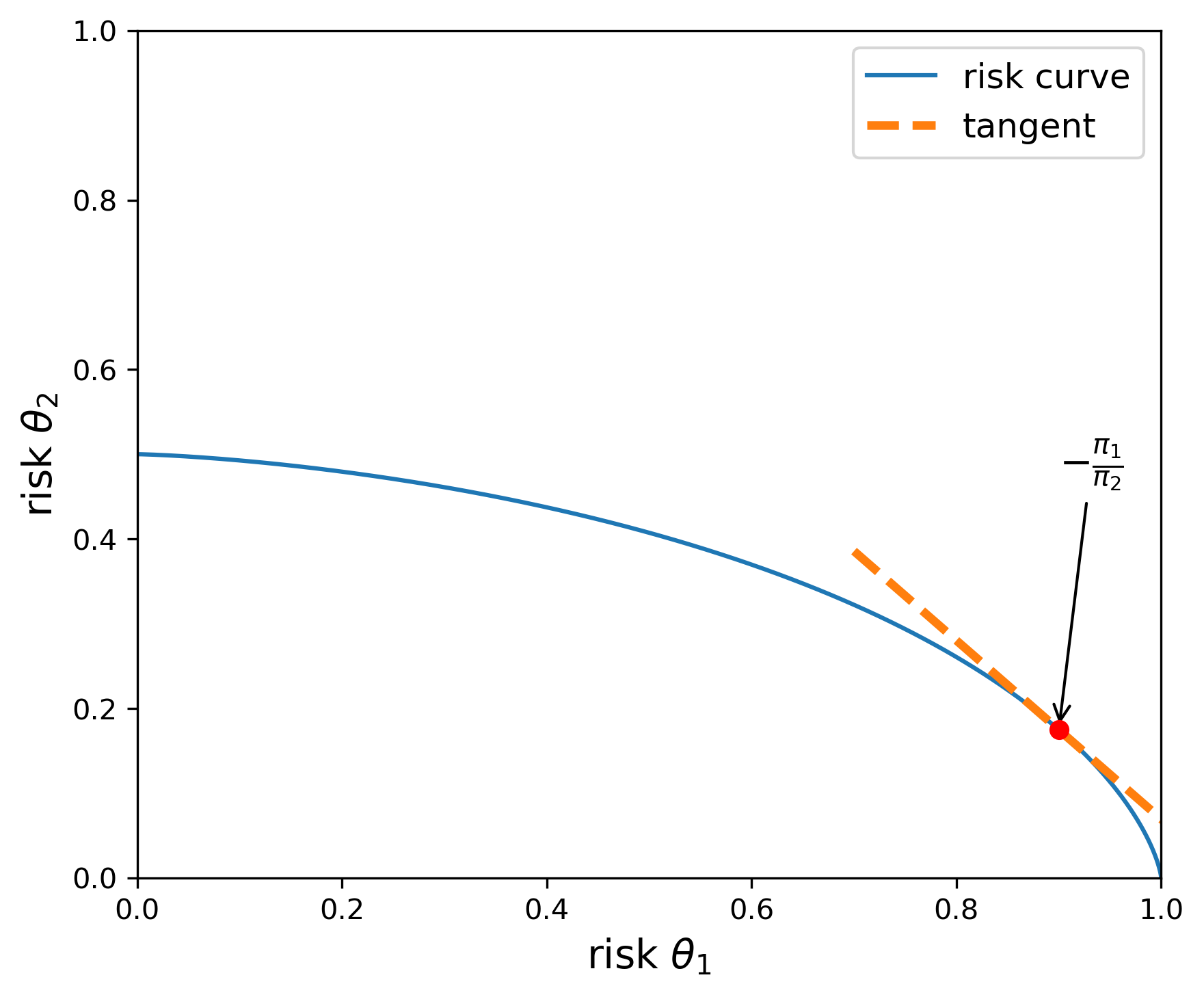
Fig. 11.2 The blue curve gives the upper boundary of the feasible set of risks. The utility function parameters are given by \(\upsilon_1= 1, \, \upsilon_2=.5.\) When \({\overline u}_{\sf r}(\theta_1) = .9\), the implied prior is given by \(\pi(\theta_1) =.51\) and \(\pi(\theta_2)=.49,\) as implied by the slope of the tangent line.

11.6. Divergences

To investigate prior sensitivity, we seek a convenient way to represent a family of alternative priors. We start with a baseline prior \(d \pi(\theta).\) Consider alternative priors of the form \(d \pi(\theta) = n(\theta) d\pi(\theta)\) for \(n \ge 0\) satisfying:

\[\int_{\Theta} n(\theta) d\pi(\theta) = 1.\]

Call this collection \({\mathcal N}\). Thus the \(n\)’s in \({\mathcal N}\) are expressed as densities relative to a baseline prior distribution.

Introduce a convex function \(\phi\) to construct a divergence between a probability represented with \(n \ne 1\) and the baseline probability. Restrict \(\phi\) to be a convex function with \(\phi(1) = 0\) and \(\phi''(1) = 1\) (normalization). As a measure of divergence, form

\[\int_\Theta \phi [n(\theta)] d \pi(\theta) \ge 0.\]

Of course, many such divergences could be built. Three interesting ones use the convex functions:

• \(\phi(n) =- \log n\)

• \(\phi(n) =\frac {n^2 -1}{2}\)

• \(\phi(n) = n \log n\)

The divergence implied from the third choice is commonly used in applied probability theory and information theory. It is called Kullback-Leibler divergence or relative entropy.

11.7. Robust Bayesian preferences and ambiguity aversion

Since the Bayesian ranking of prize rules depends on the prior distribution, we now explore how to proceed if the decision maker does not have full confidence in a specific prior. This leads naturally to an investigation of prior sensitivity. A decision or policy problem provides us with an answer to the question: sensitive to what. One way to investigate prior sensitivity is to approach it from the perspective of robustness. A robust decision rule then becomes one that performs well under alternative priors of interest. To obtain robustness guarantees, we are naturally led to minimization, providing us with a lower bound on performance. As we will see, prior robustness has very close ties to preferences that display ambiguity aversion. Just as risk aversion induces a form of caution in the presence of uncertain outcomes, ambiguity aversion induces a caution because of the lack of confidence in a single prior.

We explore prior robustness by using a version of variational preferences( [Maccheroni et al., 2006])

\[\min_{n \in {\mathcal N} } \int_\Theta \left( \int_{\mathcal X} U[\gamma(x), \theta ] \ell(x | \theta) d \tau(x) \right) n(\theta) d\pi(\theta) + \xi_1\int_\Theta \phi_1[n(\theta)] d \pi(\theta) \]

for \(\xi_1 > 0\) and a convex function \(\phi_1\) such that \(\phi_1(1)= 0\) and \({\phi_1}''(1) = 1.\) The penalty parameter \(\xi_1\) reflects the degree of ambiguity aversion. An arbitrarily large value of \(\xi_1\) approximates subjective expected utility. Relatively small values of \(\xi_1\), inducing relatively large degrees of ambiguity aversion.

Remark 11.2

Axiomatic developments of decision theory in the presence of risk typically do not produce the functional form for the utility function. That requires additional considerations. An analogous observation applies to the axiomatic development of variational preferences by [Maccheroni et al., 2006]. Their axioms do not inform as to the how to capture the cost associated with search over alternative priors.

Remark 11.3

The variational preferences of [Maccheroni et al., 2006] also include preferences with a constraint on priors:

\[\int_\Theta \phi_1[n(\theta)] d \pi(\theta) \le \kappa.\]

The more restrictive axiomatic formulation of [Gilboa and Schmeidler, 1989] supports a representation with a constraint on the set of priors. In this case we use standard Karush-Kuhn-Tucker multipliers to model the preference relation:

\[\max_{\xi_1 \ge 0} \min_{n \in {\mathcal N} } \int_\Theta \left( \int_{\mathcal X} U[\gamma(x), \theta ] \ell(x | \theta) d \tau(x)) \right) n(\theta) d\pi(\theta) + \xi_1\left[ \int_\Theta \phi_1[n(\theta)] d \pi(\theta) - \kappa\right].\]

11.7.1. Relative entropy divergence

Suppose we use \(n \log n\) to construct our divergence measure. Recall the construction of the risk function

\[{\overline {U}}(\gamma \mid \theta) = \int_{\mathcal X} U[\gamma(x), \theta] \ell(x\mid \theta ) d \tau(x) \]

Solve the Lagrangian:

\[\min_n \int_\Theta {\overline {U}}(\gamma \mid \theta) n(\theta) d \pi(\theta) + \xi_1 \int_\Theta \log n(\theta) n(\theta) d\pi(\theta) + \lambda \int_\Theta[n(\theta) -1] d \pi(\theta)\]

This problem separates in terms of the choice of \(n(\theta)\), and can be solved \(\theta\) by \(\theta\). The first-order conditions are:

\[{\overline {U}}(\gamma \mid \theta) + \xi_1 + \xi_1 \log n(\theta) + \lambda = 0.\]

Solving for \(\log n(\theta)\):

\[\log n(\theta) = - \frac 1 {\xi_1} {\overline {U}}(\gamma \mid \theta) - 1 - \frac {\lambda}{\xi_1}\]

Thus

\[n(\theta) \hspace{.2cm} \propto \hspace{.2cm} \exp\left[ - \frac 1 {\xi_1} {\overline { U}}(\gamma \mid \theta) \right].\]

Imposing the integral constraint on \(n\) gives the solution:

\[n^*(\theta) = \frac {\exp\left[ - \frac 1 {\xi_1} {\overline {U}}(\gamma \mid \theta) \right]}{\int_\Theta \exp\left[ - \frac 1 {\xi_1} {\overline { U}}(\gamma \mid \theta) \right] d \pi(\theta)}, \]

provided that the denominator is finite. This solution induces what is known as exponential tilting. The baseline probabilities are tilted towards lower values of \({\overline { U}}(\gamma \mid \theta)\). Plugging back into the minimization problem gives:

(11.10)\[- \xi_1 \log \int_\Theta \exp\left[ - \frac 1 {\xi_1} {\overline {U}}(\gamma \mid \theta) \right] d \pi(\theta). \]

This minimized objective is known to depict be a special case of smooth ambiguity preferences initially proposed by [Klibanoff et al., 2005], although these authors provide a different motivation for their ambiguity adjustment. The connection we articulate opens the door to more direct link to challenges familiar to statisticians and econometricians wrestling with how to analyze and interpret data. Indeed [Cerreia-Vioglio et al., 2013] also adopt a robust statistics perspective when exploring smooth ambiguity aversion preferences. They use constructs and distinctions of the type we explored in Chapter 1:Laws of Large Numbers and Stochastic Processes in characterizing what is and is not learnable from the Law of Large Numbers.

11.7.2. Robust Bayesian decision problem

We extend Decision Problem (11.1) to include prior robustness by introduce a special case of a two-player, zero-sum game:

Game 11.4

(11.18)\[\max_{\gamma \in \Gamma(\Delta)} \min_{n \in {\mathcal N}} \int_\Theta \left(\int_{\mathcal X} {U}[\gamma(x), \theta] \ell(x | \theta) d \tau(x) \right)n(\theta) d\pi(\theta) + \xi_1\int_\Theta \phi_1[n(\theta)] d \pi(\theta) .\]

Notice that in this formulation, the minimization depends on the choice of the decision rule \(\delta\). This is to be expected as the prior with the most adverse consequences for the expected utility should plausibly depend on the potential course of action under consideration.

For a variety of reasons, it is of interest to investigate a related problem in which the order of extremization is exchanged:

Game 11.5

(11.12)\[\min_{n \in {\mathcal N}} \max_{\gamma \in \Gamma(\Delta)} \int_\Theta \left(\int_{\mathcal X} {U}[\gamma(x), \theta] \ell(x | \theta) d \tau(x) \right)n(\theta) d\pi(\theta) + \xi_1\int_\Theta \phi_1[n(\theta)] d \pi(\theta) .\]

Notice that for a given \(n\), the inner problem is essentially just a version of the Bayesian problem (11.1). The penalty term

\[\xi_1\int_\Theta \phi_1[n(\theta)] d \pi(\theta)\]

is additively separable and does not depend on \(\delta\). In this formulation, we solve a Bayesian problem for each possible prior, and then minimize over the priors taking account of the penalty term. Provided that the outer minimization problem over \(n\) has a solution, \(n^*,\) the implied decision rule, \(\delta_{n^*},\) solves a Bayesian decision problem. As we know from section Constructing admissible decision rules, this opens the door to verifying admissibility.

The two decision games: (11.18) and (11.12) essentially have the same solution under a Minimax Theorem. That is the implied value functions are the same and \(\delta_{n^*},\) from Game (11.12) solves Game (11.18) and gives the robust decision rule under prior ambiguity. This result holds under a variety of sufficient conditions. Notice that the objective for Game (11.18) is convex in \(n\). A well known result due to [Fan, 1952] verifies the Minimax Theorem when the objective satisfies a generalization of concavity with a convex constraint set \(\Delta\). While we cannot always justify this exchange, there are other sufficient conditions that are also applicable.

A robust Bayesian advocate along the lines of [Good, 1952], view the solution, say \(n^*,\) from Game (11.12) as a choice of a prior to be evaluated subjectively. It is often referred as a “worst-case prior’’, but an object that is of interest in its own right. For an application of this idea in economics see [Chamberlain, 2000].[6] Typically, \(n^*(\theta) d\pi(\theta)\) can be computed as part of an algorithm for finding a robust decision rule, and is arguably worth serious inspection. While we could just view robustness considerations as a way to select a prior, the (penalized) worst-case solutions can instead be viewed as a device to implement robustness. While they are worthy of inspection, just as with the baseline prior probabilities, the worst-case probabilities are not intended to be a specification of a fully confident input of subjective probabilities and are dependent on the utility function and constraints imposed on the decision problem.

11.7.2.1. A simple statistical application reconsidered

We again use the model selection to illustrate ambiguity aversion in the presence of a relative entropy cost of a prior deviating from the baseline. Since the Minimax Thoerem applies, and we focus our attention on admissible decision rules parameterized by threshold decision rules of form (11.8). With this simplification, we use formula (11.10) and solve the scalar maximization problem:

\[\max_{\sf r} - \xi_1 \log \left( \exp\left[ - \frac 1 {\xi_1} {\overline u}_1({\sf r}) \right] \pi(\theta_1) + \exp\left[ - \frac 1 {\xi_1} {\overline u}_2({\sf r}) \right] \pi(\theta_2) \right)\]

Two limiting cases are of interest. When \(\xi_1 \rightarrow \infty\), the objective collapses the subjective expected utility:

\[ {\overline u}_1({\sf r}) \pi(\theta_1) + {\overline u}_2({\sf r}) \pi(\theta_2) \]

for \({\sf r}\) chosen so that the tangency condition

\[\left( \frac {\upsilon_2}{\upsilon_1} \right) \exp(-{\sf r}) = \frac {\pi(\theta_1)}{\pi(\theta_2)} \]

is satisfied.

When \(\xi_1 \rightarrow 0\), the cost of deviating from the baseline prior is zero. As long as the baseline prior assigns positive probability to both values of \(\theta\), the minimization for a given threshold \({\sf r}\) assigns probability one to lowest risk with an objective:

\[\min \{ {\overline u}_1({\sf r}) , {\overline u}_2({\sf r}) \}\]

Graphically, the objective for any point to the left of the 45 degree line from the origin equals the outcome of a vertically downward movement to that same line. Analogously, the objective for any point to the right of the 45 degree line from the origin equals the outcome of a horizontally leftward movement to that same line. Thus maximizing threshold choice of \({\sf r}\) is obtained a the intersection of the 45 degree line and the boundary of risk set. Along the 45 degree line, the choice of prior is inconsequential because the two risks are the same. Nevertheless, the “worst-case” prior is determined by slope of the risk curve at the intersection point. Recall that we defined this prior after exchanging orders of extremization. Figures Fig. 11.3 and Fig. 11.4 illustrate this outcome for the two risk curves on display in Figures Fig. 11.1 and Fig. 11.2.

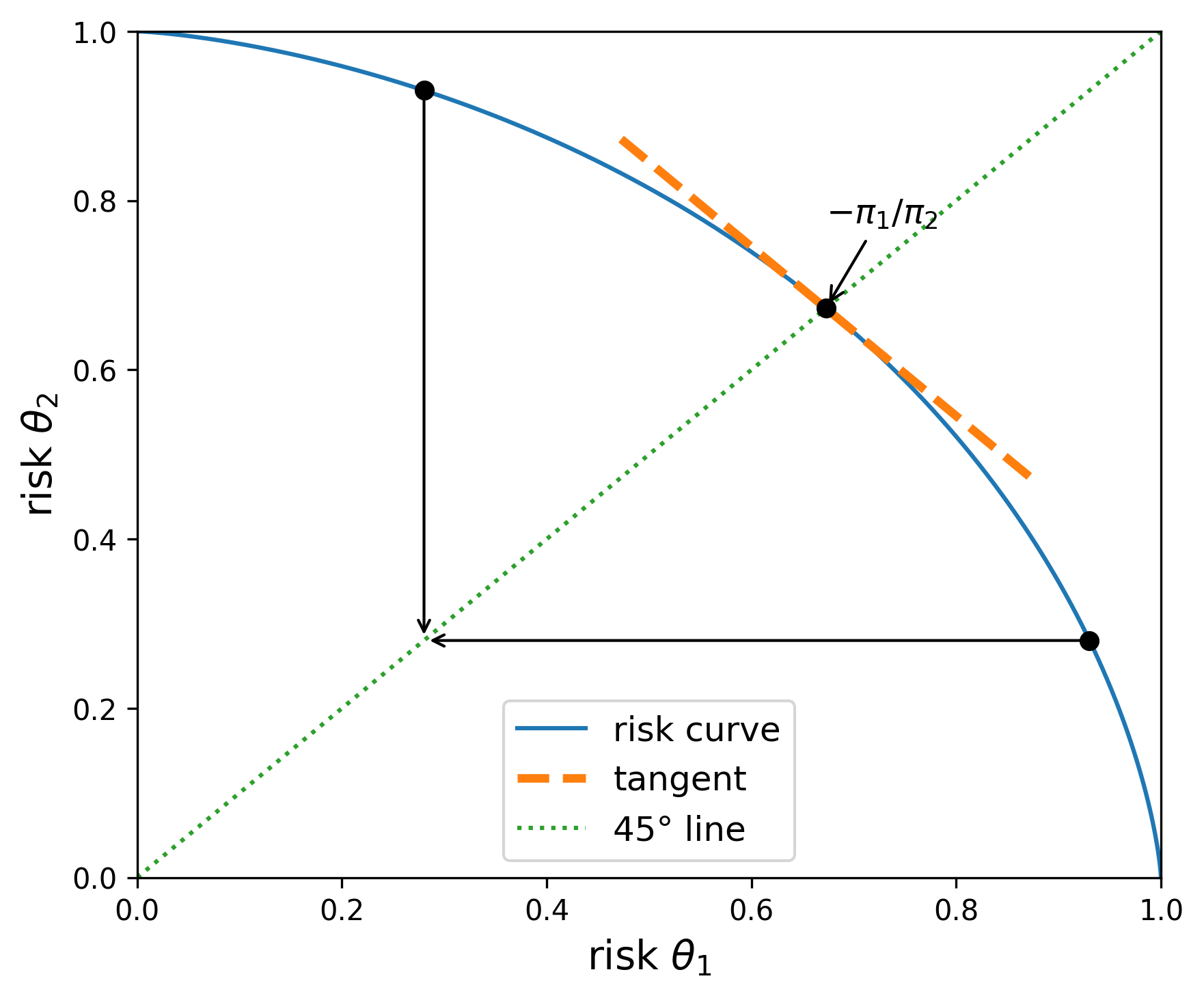
Fig. 11.3 The blue curve gives the upper boundary of the feasible set of risks. The utility function parameters are given by \(\upsilon_1=\upsilon_2=1.\) The implied worst-case prior is given by \(\pi(\theta_1) =.5\) and \(\pi(\theta_2)=.5,\) as implied by the slope of the tangent line at the intersection with the 45 degree line from the origin.

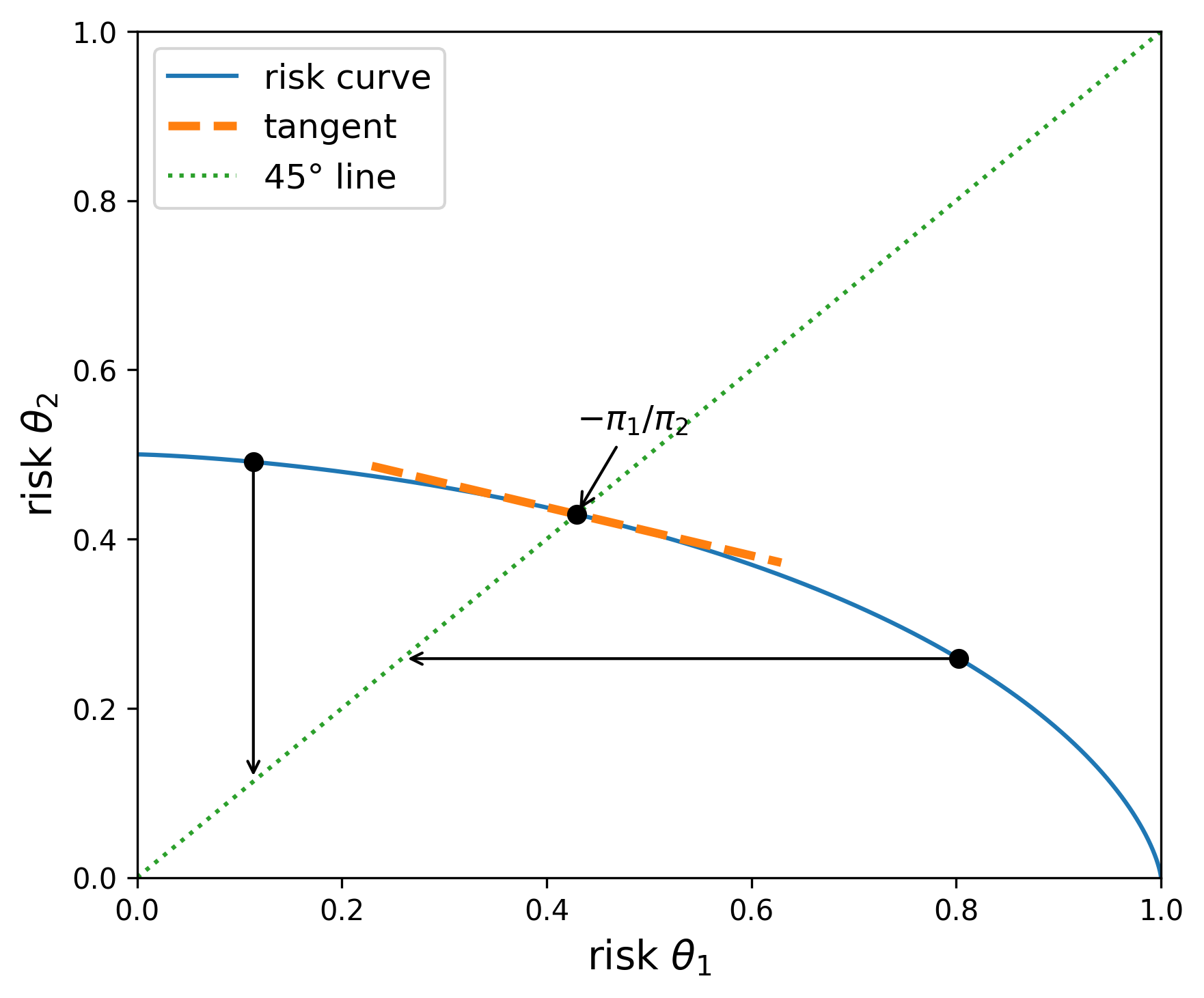
Fig. 11.4 The blue curve gives the upper boundary of the feasible set of risks. The utility function parameters are given by \(\upsilon_1\) and \(\upsilon_2=.5.\) The implied worst-case prior is given by \(\pi(\theta_1) =.22\) and \(\pi(\theta_2)=.78,\) as implied by the slope of the tangent line at the intersection with the 45 degree line from the origin.

For positive values of \(\xi_1,\) the implied worst-case priors are between the baseline \(\pi\) (\(\xi = \infty\)) and the worst-case without restricting the prior probabilities (\(\xi = 0\)). Observe that the worst-case priors depend on the utility weights, \(\upsilon_1\) and \(\upsilon_2\). See Figures Fig. 11.5 and Fig. 11.6 as illustrations.

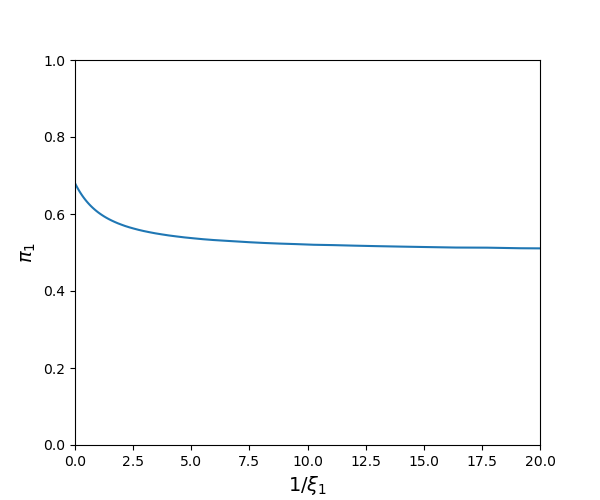
Fig. 11.5 Minimizing prior probabilities for \(\theta_1\) as a function of \(1/\xi_1\) when the baseline prior probabilities are \(\pi(\theta_1) = .68\) and \(\pi(\theta_2) = .32\) and the utility parameters are \(\upsilon_1=\upsilon_2=1.\)

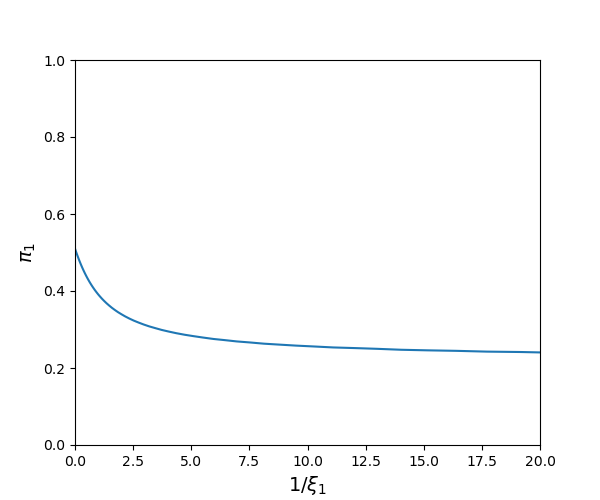
Fig. 11.6 Minimizing prior probabilities for \(\theta_1\) as a function of \(1/\xi_1\) when the baseline prior probabilities are \(\pi(\theta_1) = .51\) and \(\pi(\theta_2) = .49\) and the utility parameters are \(\upsilon_1= 1\) and \(\upsilon_2=.5.\)

The two-model example dramatically understates the potential value of ambiguity aversion as a way to study prior sensitivity. In typical applied problems, the subjective probabilities are imposed on a much richer collection of alternative models including families of models indexed by unknown parameters. In such problems the outcome is more subtle since the minimization isolates dimensions along with prior sensitivity has the most adverse impacts on the decision problem and perhaps most worthy of further consideration. This can be especially important in problems where baseline priors are imposed “as a matter or convenience.”

11.8. Using ambiguity aversion to represent concerns about model misspecification

Two prominent statisticians remarked on how model misspecification is pervasive:

“Since all models are wrong, the scientist must be alert to what is importantly wrong. It is inappropriate to be concerned about mice when there are tigers abroad.” - Box (1976).

“… it does not seem helpful just to say that all models are wrong. The very word ‘model’ implies simplification and idealization. The idea that complex physical, biological or sociological systems can be exactly described by a few formulae is patently absurd. The construction of idealized representations that capture important stable aspects of such systems is, however, a vital part of general scientific analysis and statistical models, especially substantive ones …” - Cox (1995).

Other scholars have made similar remarks. Robust control theorists have suggested on way to address this challenge, an approach that we build on in the discussion that follows. Motivated by such sentiments, [Cerreia-Vioglio et al., 2025] extend decision theory axioms to accommodate misspecification concerns.

11.8.1. Basic approach

To focus on the misspecification of specific model, we fix \(\theta\) but vary the likelihood function as a way to investigate likelihood sensitivity. We then replace \(\ell\) with \(m \ell \) satisfying:

\[\int_{\mathcal X} m(x \mid \theta) \ell(x \mid \theta) d\tau(x) = 1, \]

and denote the set of all such \(m's\) as \(\mathcal M\).

Observe that \(m(x \mid \theta)\) can be viewed as the ratio of two densities. Consider two alternative probability densities (with respect to \(d \tau(x)\) for shock/date probabilities: \(\ell(x \mid \theta)\) and \({\tilde \ell}(x \mid \theta)\) and let:

\[m( x \mid \theta) = \frac { {\tilde \ell}(x \mid \theta)}{ \ell(x \mid \theta)} \]

where we assume \(\ell(x \mid \theta) > 0\) for \(x \in {\mathcal X}\). Then by construction:

\[m(x \mid \theta) \ell(x \mid \theta) = {\tilde \ell}(x \mid \theta),\]

and

\[\int_{\mathcal X} m(x \mid \theta) \ell( x \mid \theta) d \tau(x) = \int_{\mathcal X} {\tilde \ell}(x \mid \theta) d \tau(x) = 1.\]

We use density ratios to capture alternative models as inputs into divergence measures. Let \(\phi_2\) be a convex function such that \({\phi_2}(1) = 0\) and \({\phi_2}''(1) = 1\) (normalization). Instead of imposing the divergence over the probabilities over the parameter space, to explore misspecification, impose it over the \({\mathcal X}\) space:

\[\int_{\mathcal X} \phi_2\left[ m(x \mid \theta) \right] d \tau(x). \]

We use this divergence to limit or constrain our search over alternative probability models. In this approach we deliberately avoid imposing a prior distribution over the space of densities (with respect to \(d \tau(x))\).

Preferences for model robustness ranks alternative prize rules, \(\gamma\), by solving:

(11.13)\[\min_{m \in {\mathcal M}} \int_{\mathcal X} \left( U[\gamma(x), \theta]m(x \mid \theta) + \xi_2 \phi_2[m(x \mid \theta) ]\right) \ell(x \mid \theta) d\tau(x). \]

for a penalty parameter \(\xi_2 > 0.\) The parameter, \(\xi_2\), dictates the strength of the restraint in an exploration of possible model misspecifications.

11.8.2. Relative entropy divergence

This approach to model misspecification has direct links to robust control theory in the case of relative entropy divergence. Suppose that \(\phi_2(m) = m \log m\) (relative entropy). Then by imitating previous computations, we find that the outcome of the minimization in (11.13) is

\[- \xi_2 \log \int_{\mathcal X} \exp \left[ - \left(\frac 1 {\xi_2}\right) U[\gamma(x), \theta] \right] \ell(x \mid \theta) d \tau(x) \]

Remark 11.4

Robust control emerged from the study optimization of dynamical systems. The use of the relative entropy divergence showed up prominently in [Jacobson, 1973] and later in [Whittle, 1981], [Petersen et al., 2000] and many other related papers as a response to the excessive simplicity of assuming shocks to dynamical systems that were iid and mean zero with normal distributions. [Hansen and Sargent, 1995] and [Hansen and Sargent, 2001] showed to how to reformulate the insights from robust control theory to apply to dynamical economic systems with recursive formulations and [Hansen et al., 1999] used this ideas in an initial empirical investigation.

When we use relative entropy as a measure of divergence, we have the ability to factor likelihoods in convenient ways. Recall that partitioning of \(x = (w, z)\) where the decision rule can only depend on \(z\) and the prize rule on the entire \(x\) vector. As in (11.2), factor \(\ell(\cdot \mid \theta)\) and \(\tau\) as:

\[\begin{split} d \tau(x) & = d \tau_2(w) d\tau_1(z) \cr \ell(x \mid \theta) & = \ell_2(w \mid z, \theta) \ell_1(z \mid \theta) . \end{split}\]

Add to this a factorization of \(m(\cdot \mid \theta)\),

(11.14)\[\begin{split} & \hspace{1cm} m(x \mid \theta) = m_2(w \mid z, \theta) m_1(z \mid \theta) \cr & \int_{\mathcal W} m_2( w \mid \theta, z) \ell_2( w \mid \theta, z) d \tau_2(w) = 1\cr & \int_{\mathcal Z} m_1( z \mid \theta) \ell_1( z \mid \theta) d \tau_1(z) = 1 \end{split}\]

Let \({\mathcal M}_1\) denote the set of \(m_1(z \mid \theta) \ge 0\) that satisfy the relevant integral constraint in (11.14), and similarly let \({\mathcal M}_2\) be the set of \(m_2(w \mid z, \theta) \ge 0\) that satisfy the relevant integral constraint.

Using these factorizations, the relative entropy may be written as:

\[\begin{split} &\int_{\mathcal Z} \int_{\mathcal W} \log[m_2(w \mid z, \theta)] m(x \mid \theta) \ell(x \mid \theta) d \tau(x) \cr & + \int_{\mathcal Z} \log[m_1(z \mid \theta)] m_1(z \mid \theta) \ell_1(z \mid \theta) d \tau_1(z) \end{split} \]

In particular,

(11.15)\[\begin{split} & \int_{\mathcal Z} \int_{\mathcal W} \log[m_2(w \mid z, \theta)] m(x \mid \theta) \ell(x \mid \theta) d \tau(x) \cr & = \int_{\mathcal Z} \left[ \int_{\mathcal W} \log[m_2(w \mid z, \theta)]m_2(w \mid z, \theta)\ell_2(w \mid z, \theta) d\tau_2(w) \right] \cr & \hspace{2cm}\times m_1(z \mid \theta) \ell_1(z \mid \theta) d \tau_1(z). \end{split}\]

Rewrite the expected utility function in (11.13) with an inner integral:

(11.16)\[\begin{split} \int_{\mathcal Z} & \left[\int_{\mathcal W} U\left(\Psi\left[\delta(z), w, z\right], \theta \right) m_2(w \mid z, \theta) \ell_2(w \mid z, \theta) d \tau_2(w) \right] \cr & \hspace{.8cm} \times m_1(z \mid \theta) \ell_1(z \mid \theta) d \tau_1(z) \end{split}\]

Notice that both the formulas (11.15) and (11.16) scale linearly in \(m_1(z \mid \theta)\) and that the additional relative entropy term depends only on \(z\). Thus we can use a conditional objective when solving for robust decision rule \(\delta\):

Game 11.6

(11.17)\[\begin{split} \max_{\delta(z) \in \Delta(z)} \min_{m_2 \in {\mathcal M}_2} & \int_{\mathcal W} U\left(\Psi\left[\delta(z), w, z\right], \theta \right) m_2(w \mid z, \theta) \ell_2(w \mid z, \theta) d \tau_2(w)\cr & + \xi_2 \int_{\mathcal W} \log[m_2(w \mid z, \theta) ] m_2(w \mid z, \theta) \ell_2(w \mid z, \theta) d \tau_2(w) \end{split}\]

where constraint set \(\Delta\) satisfies the separability constraint (11.3).

11.8.3. Robust prediction under misspecification

A decision rule is chosen to forecast

\[f(w, z) = f_1(z) + f_2(z)w\]

where the probability distribution over the \(w\)’s is a standard normal. The admissible forecast rules expresses \(\delta\) as a function of the data \(z\). A prize rule gives the implied forecast error, \(\gamma (x)= f(x) - \delta(z)\). Take the utility function to be:

\[- {\frac 1 2} \gamma(x)^2 = - {\frac 1 2}[ f(x) - \delta(z)]^2. \]

We find the robust forecasting rule by solving Game (11.17). We first solve the inner minimization problem which is given by:

\[-\xi_2 \log E \left( \exp\left[ \left( \frac 1 {2 \xi_2} \right) \left[f_1(z) + f_2(z)w - \delta(z)\right]^2 \right] \mid z, \theta \right) .\]

To compute this objective, two exponentials contribute to this objective: one from the normal density for \(w\) and the other from the decision maker objective scaled by: \(- 1 / \xi_2\). Adding together the logarithms of these two components:

\[\begin{split} & \left( \frac 1 {2 \xi_2} \right) \left[f_1(z) + f_2(z)w - \delta(z)\right]^2 - {\frac 1 2} w^2 \cr & = {\frac 1 2}\left[ \left( \frac 1 {\xi_2} \right) [f_2(z)]^2 - 1\right]w^2 + \frac 1 {\xi_2} f_2(z) [f_1(z) - \delta(z)] w + \frac 1 {2 \xi_2} [f_1(z) - \delta(z)]^2 \cr & = - {\frac 1 2} \sf{pr} \left( w - \sf{m} \right)^2 + {\frac 1 2} \sf{pr} (\sf{m})^2 + \frac 1 {2 \xi_2} [f_1(z) - \delta(z)]^2 \cr & = \left[ - {\frac 1 2} \sf{pr} \left( w - \sf{m} \right)^2 + {\frac 1 2} \log \sf{pr}\right] + {\frac 1 {2 }} \frac { [f_1(z) - \delta(z)]^2}{\xi_2 - [f_2(z)]^2} - \frac 1 2 \log \sf{pr} \end{split} \]

where

\[\begin{split} \sf{ pr} & \eqdef 1 - \left( \frac 1 {\xi_2} \right) [f_2(z)]^2 \cr \sf{m} & \eqdef \frac { f_2(z) [f_1(z) - \delta(z)]}{ \xi_2 - [f_2(z)]^2 }. \end{split}\]

The first term in the square brackets is the logarithm of a normal density with mean \(\sf{m}\) and precision \(\sf{pr}\) except for a constant term, one that is contributed by the standard normal density. This same normal distribution is the “worst-case” distribution for forecasting rule \(\delta(z)\). For the objective to be finite, we need that

\[\xi_2 > [f_2(z)]^2\]

Given this calculation, the outcome of the minimization problem can be rewritten as

\[- \left(\frac {\xi_2} 2\right) \frac { [f_1(z) - \delta(z)]^2}{\xi_2 - [f_2(z)]^2} + \frac {\xi_2} 2 \log \left[ 1 - \left( \frac 1 {\xi_2} \right) [f_2(z)]^2\right] . \]

Maximizing with respect to \(\delta(z)\) implies that \(\delta(z) = f_1(z)\) with the resulting objective function given by:

\[- \frac {\xi_2} 2 \log \left[ 1 - \left( \frac 1 {\xi_2} \right) [f_2(z)]^2\right] < \frac 1 2 f_2(z)^2\]

Thus for this example the robust prediction is to set \(\delta(z)\) equal to the conditional mean under the baseline distribution. Robustness considerations only alter the final objective, and not the decision rule. This calculation, however, relies heavily on the normal baseline distribution.

11.9. Robust Bayes with model misspecification

To relate to decision theory, think of a statistical model as implying a compound lottery. Use \(\ell(x \mid \theta) d\tau(x) \) to as a lottery conditioned on \(\theta\) and think \(d\pi(\theta)\) as a lottery over \(\theta\). Initially we thought of the first as a source of “risk” and it gave rise to what statisticians call a risk function: the expected utility (or loss) conditioned on the unknown parameter. In the Anscombe-Aumann metaphor, this is the “roulette wheel”. The distribution, \(d \pi(\theta)\), is subjective probability input and the “horse race” in the Anscombe-Aumann metaphor. The potential misspecification of likelihoods adds skepticism of the risk contribution to the compound lottery. As statisticians like Box and Cox observed, potential model misspecification arguably should be a pervasive concern.

11.9.1. Approach one

Form a convex, compact constraint set of prior probabilities, \({\mathcal N} \subset {\mathcal N}_o\). Represent preferences over \(\gamma\) using:

\[\begin{split}\begin{aligned} \min_{n \in {\mathcal N}_o } \min_{m \in {\mathcal M}} & \int_\Theta \left( \int_{\mathcal X} U[\gamma(x), \theta] m(x \mid \theta) \ell(x \mid \theta ) d \tau_o(x) \right) n(\theta) d\pi (\theta) \\ & + \xi_2\int_\Theta \left( \int_{\mathcal X} \phi_2[m(x \mid \theta)] \ell(x \mid \theta) d\tau(x) \right) n(\theta) d \pi(\theta) \end{aligned}\end{split}\]

11.9.2. Approach two

Represent preferences over \(\gamma\) with:

\[\begin{split}\begin{aligned} \min_{n \in {\mathcal N} } \min_{m \in {\mathcal M}} & \int_\Theta \left( \int_{\mathcal X} U[\gamma(x), \theta] m(x \mid \theta) \ell(x\mid \theta ) d \tau_o(x) \right) n(\theta) d\pi (\theta) \\ & + \xi_2\int_\Theta \left( \int_{\mathcal X} \phi_2[m(x \mid \theta)] \ell(x \mid \theta) d\tau_o(x) \right) n(\theta) d \pi(\theta) \\ & + \xi_1 \int_\Theta \phi_1[n(\theta)] d\pi(\theta) \end{aligned}\end{split}\]

Note that this approach uses a scaled version of a joint divergence over \((m,n),\) as reflected in the term

\[\xi_2\int_\Theta \left( \int_{\mathcal X} \phi_2[m(x \mid \theta)] \ell(x \mid \theta) d\tau (x) \right) n(\theta) d \pi(\theta) + \xi_1 \int_\Theta \phi_1[n(\theta)] d\pi(\theta) \]

The associated decision problem is:

Game 11.6

(11.18)\[\begin{split} \max_{\gamma \in \Gamma} \min_{n \in {\mathcal N}} \min_{ m \in {\mathcal M} } & \int_\Theta \left(\int_{\mathcal X} {U}[\gamma(x), \theta] m(x \mid \theta) \ell(x | \theta) d \tau(x) \right)n(\theta) d\pi_o(\theta)\cr & + \xi_2 \int_\Theta \left( \int_{\mathcal X} \phi_2[m(x \mid \theta)] \ell(x \mid \theta) d\tau (x) \right) n(\theta) d \pi(\theta) \cr & + \xi_1\int_\Theta \phi_1[n(\theta)] d \pi(\theta) . \end{split}\]

Remark 11.5

In Section Robust prediction under misspecification we studied a prediction problem under misspecification and established the conditional expectation under the base-line model is “robust.” Now suppose there is parameter uncertainty in the sense that we have multiple specifications of the pair \((f_1(z \mid \theta), f_2(z \mid \theta) )\) for \(\theta \in \Theta\). For starters, for each \(\theta\) the ex ante contribution to the decision maker objective conditioned on a model is:

\[ -\xi_2 \log E \left( \exp\left[ \left( \frac 1 {2 \xi_2} \right) \left[f_1(z \mid \theta) + f_2(z \mid \theta)w - \delta(z)\right]^2 \right] \mid \theta \right) .\]

This objective adjusts for likelihood (or model) uncertainty but not prior uncertainty. The conditional expectation uses the probability measure; \(\ell(x \mid \theta) d\tau(x).\). Since \(\theta\) is unknown, the decision rule, \(\delta(z) = f_1(z \mid \theta)\) is infeasible to implement. Game (11.18) provides an algorithm for deducing the robust decision rule with

\[\begin{split} &\max_{\delta \in \Delta} \min_{n \in {\mathcal N}} \cr & -\xi_2 \int_\theta \log E \left( \exp\left[ \left( \frac 1 {2 \xi_2} \right) \left[f_1(z \mid \theta) + f_2(z \mid \theta)w - \delta(z)\right]^2 \right] \mid \theta \right) n(\theta) d \pi(\theta) \cr & + \xi_1 \int_\Theta \log [n(\theta)] n(\theta) d \pi(\theta). \end{split}\]

Consider the special case in which \(\xi_1 = \xi_2 = \xi,\) and use this common parameter to scale a relative entropy divergence. Then the combined robustness cost to preferences is measured by \(\xi\) multiplying the relative entropy of the joint distribution \(m(x \mid \theta) n(\theta) \ell(x \mid \theta) d\tau(x) d\pi(\theta) \) relative to the baseline \(\ell(x \mid \theta) d\tau(x) d\pi(\theta)\) and given by:

\[\begin{split}\int_\Theta \left( \int_{\mathcal X} \log[m(x \mid \theta)] m(x \mid \theta) \ell(x \mid \theta) d\tau(x) \right) n(\theta) d \pi(\theta) \\ + \int_\Theta \log [n(\theta)] n(\theta) d\pi(\theta) \end{split}\]

Joint densities can be factored in alternative ways. In solving the robust decision problem, a different factorization is more convenient. We focus on the case in which \(x = (w, z)\) and the decision rule, \(\delta,\) depends only on \(z\). Form three contributions the joint density under the baseline:

\[\begin{split} \ell(x \mid \theta) d\tau(x) d\pi(\theta) & = \ell_2(w \mid z, \theta) \ell_1(z \mid \theta) d \tau_2(w) d\tau_1(z) d\pi(\theta) \cr & = \ell_2(w \mid z, \theta) d \tau_2(w) d{\bar \pi}(\theta \mid z) \left[ \int \ell_1(z \mid \theta) d\pi(\theta) \right]d\tau_1(z). \end{split}\]

Notice that the last term in the factorization depends only on \(z,\) whereas the decision rule conditions on \(z.\) We now explore likelihood misspecification using \(m_2(w \mid z, \theta)\) satisfying:

\[\int_{\mathcal W} m_2( w \mid z, \theta) \ell_2( w \mid z, \theta) d \tau_2(w) = 1\]

and posterior misspecification using \({\bar n}(\theta \mid z )\) where

\[\int_\Theta {\bar n}(\theta \mid z ) d{\bar \pi}(\theta \mid z ) = 1.\]

Additionally, we may alter the density

\[ \int_{\Theta} \ell_1(z \mid \theta) d\pi(\theta)\]

in an analogous way. While this latter exploration will have a nondegenerate outcome, but it will have no impact on the robustly optimal choice of \(\delta\). We may instead focus on a conditional counterpart to Game (11.18). The logic behind this is entirely analogous to the argument we provided for the conditional version of the Bayesian decision problem. The objective for conditional robust game with the same solution as the ex ante game is:

Game 11.7

\[\begin{split}\begin{split} \max_{\delta(z) \in \Delta(z)} & \min_{{\bar n} \in {\overline {\mathcal N}} } \min_{m_2 \in {\mathcal M}_2} \cr & \int_\Theta \left( \int_{\mathcal W} U\left(\Psi[\delta(z), w, z], \theta \right) m_2(w \mid z, \theta) \ell_2(w\mid z, \theta ) d \tau_2(w) \right) {\bar n}(\theta \mid z) d{\bar \pi} (\theta \mid z) \\ & + \xi \int_\Theta \left( \int_{\mathcal W} \log [m_2(w \mid z, \theta )] m_2(w \mid z, \theta) \ell_2(w \mid z, \theta) d\tau_2(w) \right) {\bar n}(\theta \mid z ) d {\bar \pi}(\theta \mid z) \\ & + \xi \int_\Theta \log [{\bar n}(\theta \mid z)] {\bar n}(\theta \mid z) d{\bar \pi}(\theta \mid z) \end{split}\end{split}\]

where constraint set \(\Delta\) satisfies the separability constraint (11.3).

Thus the decision maker may proceed with constructing a robustly optimal decision rule taking as input the posterior distribution defined on a parameter space \(\Theta\) as computed by a statistician. The decision maker explores the robustness of the posterior and density for the shocks conditioned on \((z, \theta).\)

Finally, suppose that \(U\) does not depend on \(\theta\). This provides a further simplification. In this case, instead of working with the factorization:

\[\ell_2(w \mid z, \theta) d\tau_2(w) d {\bar \pi}(\theta \mid z)\]

we use

\[d{\tilde \pi}(\theta \mid w, z) {\bar \ell}_2(w \mid z) d\tau_2(w) \]

where

\[{\bar \ell}_2(w \mid z) \eqdef \int_{\mathcal{Z}} \ell_2(w \mid z, \theta) d\tau_2(w) d {\bar \pi}(\theta \mid z) \]

\(\textcolor{red}{\text{I guess we should remove} \; d\tau_2(w) \; \text{in the last integral? }}\)

\(d{\tilde \pi}(\theta \mid x)\) is posterior distribution formed using data on both \(z\) and \(w\). Statisticians call \({\bar \ell}_2(\cdot \mid z)\) a predictive density, in this case defined on the space \({\mathcal W}\) of shocks. With this alternative factorization, the minimization step has no incentive to explore the misspecification of \(d{\tilde \pi}(\theta \mid x),\) and instead focuses exclusively on the potential misspecification of the predictive density. This leads to the following construction of a robust decision rule:

Game 11.8

\[\begin{split} \max_{\delta(z) \in \Delta(z)} \min_{{\bar m}_2(w \mid z) \in {\overline {\mathcal M}}_2 } & \int_{\mathcal W} U\left(\Psi[\delta(z), w, z] \right) {\bar m}_2(w \mid z) {\bar \ell}_2(w \mid z ) d \tau_2(w) \cr & + \xi \int_{\mathcal W} \log [{\bar m}_2(w \mid \ z)] {\bar m}_2(w \mid z) {\bar \ell}_2(w \mid z) d\tau_2(w) \end{split}\]

where constraint set \(\Delta\) satisfies the separability constraint (11.3).

[Chamberlain, 2020] features this as a way to formulate preferences with uncertainty aversion.

In many applications it will be of considerable interest to allow for \(\xi_1 \ne \xi_2,\) in which case the simplifications implied by some of these alternative factorizations will not be applicable. Indeed we find it valuable and revealing to differentiate prior robustness and likelihood robustness.[7]

11.10. A dynamic decision problem under commitment

So far, we have studied static decision problems. This formulation can accommodate dynamic problems by allowing for decision rules that depend on histories of data available up until the date of the decision. While there is a “commitment” to these rules at the initial date, the rules themselves can depend on pertinent information only revealed in the future. Recall from Chapter 1, that we use an ergodic decomposition to identify a family of statistical models that are dynamic in nature along with probabilities across models that are necessarily subjective as they are not revealed by data.

We illustrate how we can use the ideas in this “static” chapter to study a macro-investment problem with parameter uncertainty.

Consider an example of a real investment problem with a single stochastic option for transferring goods from one period to another. This problem could be a planner’s problem supporting a competitive equilibrium outcome associated with a stochastic growth model with a single capital good. Introduce an exogenous stochastic technology process that has an impact on the growth rate of capital as an example of what we call a structured model. This stochastic technology process captures what a previous literature in macro-finance has referred to as “long-run risk.” For instance, see [Bansal and Yaron, 2004].[8]

We extend this formulation by introducing an unknown parameter \(\theta\) used to index members of a parameterized family of stochastic technology processes. The investor’s exploration of the entire family of these processes reflects uncertainty among possible structured models. We also allow the investor to entertain misspecification concerns over the parameterized models of the stochastic technology.

The exogenous (system) state vector \(Z_{t}\) used to capture fluctuations in the technological opportunities has realizations in \({\mathcal Z}\) and the shock vector \(W_{t}\) has realizations in \({\mathcal W}\). We build the exogenous technology process from the shocks in a parameter dependent way:

\[Z_{t+1}=\psi \left( Z_{t},W_{t+1},\theta \right) \]

for a given initial condition \(Z_{0}\).

For instance, in long-run risk modeling one component of \(Z_{t}\) evolves as a first-order autoregression:

\[Z_{t+1}^{1}= {\mathbf a}_{\theta}Z_{t}^{1}+{\mathbf b}_{\theta}^{1}\cdot W_{t+1}\]

and another component is given by:

\[Z_{t+1}^{2}={\mathbf d}_{\theta}+{\mathbf c}_{\theta}^{2}\cdot W_{t+1}\]

At each time \(t\) the investor observes past and current values \(\mathbf{Z} ^{t}=\left \{ Z_{0},Z_{1},...,Z_{t}\right \} \) of the technology process, but does not know \(\theta\) and does not directly observe the random shock vector \(W_{t}\).

Similarly, we consider a recursive representation of capital evolution given by:

\[K_{t+1} = K_{t}\varphi \left( I_{t}/K_{t},Z_{t+1}\right)\]

where consumption \(C_{t}\geq0\) and investment \(I_{t}\geq0\) are constrained by an output relation:

\[C_{t}+I_{t}=\alpha K_{t}\]

for a pre-specified initial condition \(K_{0}\). The parameter \(\alpha\) captures the productivity of capital. By design this technology is homogeneous of degree one, which opens the door to stochastic growth as assumed in long-run risk models.

Both \(I_{t}\) and \(C_{t}\) are constrained to be functions of \(\mathbf{Z}^{t}\) at each date \(t\) reflecting the observational constraint that \(\theta\) is unknown to the investor in contrast to the history \(\mathbf{Z}^{t}\) of the technology process.[9] Preferences are defined over consumption processes.

In this intertemporal setting, we consider an investor who solves a date \(0\) commitment problem. We pose this as a static problem with consumptions and investments that depend on information as it gets realized.[10] Form the risk function

\[(1 - \beta) E \left[ \sum_{t=0}^\infty \beta ^t \upsilon(C_t) \mid K_0, Z_0 , \theta \right]. \]

While the initial conditions \(K_0\) and \(Z_0\) are known, the parameter vector \(\theta\) is not.

Include divergences, one for the parameter \(\theta\) and the other for the potential misspecification in the dynamics as reflected in the shock distributions. The latter divergence will necessarily be dynamic in nature. We will use positive random variables with unit expectations as a way to introduce changes in probabilities. Introduce a positive martingale \(\{ M_t : t \ge 0 \}\) for an altered probability. Let \(M_0=1\) and let \(M_t\) depend on state variables and shocks up to period \(t\) along with \(\theta\). We use the random variable \(M_t\) alter date \(t\) probabilities conditioned on \(K_0, Z_0, \theta\). The martingale property ensures that the altered probabilities implied by \(M_{t+1}\) agree with the altered probabilities implied by \(M_t\) as an implication of the Law of Iterated Expectations. Let the intertemporal divergence be:

\[(1-\beta) E \left( \sum_{t=0}^\infty \beta^t M_{t+1} \log M_{t+1} \mid K_0, Z_0, \theta \right)\]

as a measure of divergence and scale this by a penalty parameter, \(\xi_2\). We purposefully discount the relative entropies in the same way as we discount the utility function and the computations condition on \(\theta\). We then use a second divergence over the parameter vector \(\theta\) with a penalty parameter \(\xi_1.\)

In this model, the investor or planner will actively learn about \(\theta\). The potential model misspecifications are not linked over time and presumed not to be learnable. This model formulation presumes a preference for prior and likelihood robustness. Unfortunately it does not have a convenient recursive formulation, making it challenging to solve.

11.11. Recursive counterparts

We comment briefly on recursive counterparts. We have seen in the previous chapter how to perform recursive learning and filtering. Positive martingales also have a convenient recursive structure. Write:

\[\log M_{t+1} = \sum_{j=1}^t \log M_{j+1} - \log M_{j} \]

By the Law of Iterated Expectations:

(11.19)\[\begin{split} E\left(M_{t+1} \log M_{t+1} \mid {\mathfrak A}_0 \right) & = E \left[ M_{t+1} \left( \sum_{j=0}^t \log M_{j+1} - \log M_{j}\right) \mid {\mathfrak A}_0 \right] \cr & = E \left[ \sum_{j=0}^t M_{j+1}\left( \log M_{j+1} - \log M_{j}\right) \mid {\mathfrak A}_0 \right] \cr & = E \left[ \sum_{j=0}^t M_{j} \left(\frac {M_{j+1}}{M_{j}} \right)\left( \log M_{j+1} - \log M_{j}\right) \mid {\mathfrak A}_0 \right] \cr & = E \left( \sum_{j=0}^t M_{j} E\left[\left(\frac {M_{j+1}}{M_{j}} \right)\left( \log M_{j+1} - \log M_{j}\right) \mid {\mathfrak A}_{j}\right] \mid {\mathfrak A}_0 \right). \end{split}\]

Using this calculation and applying “summation-by-parts” (implemented by changing the order of summation) gives:

\[\begin{split} & (1-\beta) E \left( \sum_{t=0}^\infty \beta^t M_{t+1} \log M_{t+1} \mid {\mathfrak A}_0\right) \cr & = (1-\beta) \sum_{t=0}^\infty \beta^{t} E \left( \sum_{j=0}^t M_{j} E\left[\left(\frac {M_{j+1}}{M_{j}} \right)\left( \log M_{j+1} - \log M_{j}\right) \mid {\mathfrak A}_{j}\right] \mid {\mathfrak A}_0 \right)\cr & = \sum_{t=0}^\infty \beta^{t} E \left( M_{t} E\left[\left(\frac {M_{t+1}}{M_{t}} \right)\left( \log M_{t+1} - \log M_{t}\right)\mid {\mathfrak A}_{t}\right] \mid {\mathfrak A}_0 \right) \end{split}\]

In this formula,

\[ E\left[\left(\frac {M_{t+1}}{M_{t}} \right)\left( \log M_{t+1} - \log M_{t}\right)\mid {\mathfrak A}_{t}\right]\]

is relative entropy pertinent to the transition probabilities between date \(t\) and \(t+1\). With this formula, we form a discounted objective with date \(t\) contribution to confront potential likelihood misspecification:

\[\upsilon( C_t) + \beta \xi_2 E\left[\left(\frac {M_{t+1}}{M_{t}} \right)\left( \log M_{t+1} - \log M_{t}\right)\mid {\mathfrak A}_{t}\right]\]

where date \(t\) minimizing choice variable is \(M_{t+1}/M_{t} \ge 0\) subject to \(E\left(M_{t+1}/M_{t} \mid {\mathfrak A}_t \right) = 1.\) The ratio \(M_{t+1}/M_{t}\) is used when computing the conditional expectation of next periods continuation value needed to rank current period actions.

Remark 11.6

Our discounting of relative entropy has important consequences for exploration of potential misspecification. From (11.19), it follows that the sequence

(11.20)\[\left\{ E \left( M_t \log M_t \mid {\mathfrak A}_0 \right) : t\ge 0 \right\}\]

is increasing in \(t\). Observe that

(11.21)\[\lim_{\beta \uparrow 1} \hspace{.2cm} (1-\beta) E \left( \sum_{t=0}^\infty \beta^t M_{t+1} \log M_{t+1} \mid {\mathfrak A}_0\right) \]

gives an upper bound on

\[E \left( M_{s+1} \log M_{s+1} \mid {\mathfrak A}_0\right)\]

for each \(s \ge 0\). This follows from monotonicity since

\[\begin{split} (1-\beta) E \left( \sum_{t=0}^\infty \beta^t M_{t+1} \log M_{t+1} \mid {\mathfrak A}_0\right) & \ge (1-\beta) \sum_{t=s}^\infty \beta^{t} E \left( M_{t+1} \log M_{t+1} \mid {\mathfrak A}_0\right)\cr & = \beta^s E \left( M_{s+1} \log M_{s+1} \mid {\mathfrak A}_0\right) \end{split}\]

Taking limits as \(\beta \uparrow 1\) gives the bound of interest.

If the discounted limit in (11.21) is finite, then the increasing sequence (11.20) has a finite limit. It follows from a version of the Martingale Convergence Theorem (see [Barron, 1990]), that there is limiting random nonnegative variable \(M_\infty\) such that \(E \left( M_\infty \mid {\mathfrak A}_0 \right) =1\) and

\[M_t = E \left(M_\infty \mid {\mathfrak A}_t \right). \]

Observe that in the limiting case when \(\beta \uparrow 1\) and the resulting relative entropy measure is finite, the altered probability must imply Law of Large Numbers that agrees with the baseline probability. In this sense only transient departures from the baseline probability are part of the misspecification exploration. By including discounting in the manner described, we expand the family of alternative probabilities in a substantively important way.

As an alternative calculation, consider a different discount factor scaling:

\[(1-\beta) \sum_{t=0}^\infty \beta^t E \left( M_{t} E\left[\left(\frac {M_{t+1}}{M_{t}} \right)\left( \log M_{t+1} - \log M_{t}\right)\mid {\mathfrak A}_{t}\right] \mid {\mathfrak A}_0 \right)\]

The limiting version of this measures allows for substantially larger set of alternative probabilities and results in limiting characterization that is used in Large Deviation Theory as applied in dynamic settings.

Remark 11.7

To explore potential misspecification [Chen et al., 2020] suggest other divergences with convenient recursive structures. A discounted version of their proposal is

\[(1-\beta) E \left[ \sum_{j=0}^t \beta^t E\left[M_t \phi_2\left( M_{t+1}/M_{t}\right) \mid {\mathfrak A}_t\right] \mid {\mathfrak A}_0 \right] \]

for a convex function \(\phi_2\) where this function equals one when evaluated at one and its second derivative at one is normalized to be one.

11.12. Implications for uncertainty quantification

Uncertainty quantification is a challenge that pervades many scientific disciplines. The methods we describe here open the door to answering the “so what” aspect of uncertainty measurement. So far, we have deliberately explored examples that are low-dimensional to illustrate results. While these are pedagogically revealing, the methods we described have all the more potency in problems with high-dimensional uncertainty. By including minimization as part of the decision problem, we isolate the uncertainties that are of most relevance to the decision or policy problem. This may open the door to incorporating sharper prior inputs or to guiding future efforts aimed at providing additional evidence relevant to the decision-making challenge. Furthermore, there may be multiple channels by which uncertainty can impact the decision problem. As an example consider an economic analysis of climate change. There is uncertainty in i) the global warming implications of increases in carbon emissions, ii) the impact of global warming on economic opportunities, and iii) the prospects for the discovery of new, clean technologies that are economically viable. A direct extension of the methods developed in this chapter provide a (non-additive) decomposition the channel uncertainty. By modifying the penalization, uncertainty in each channel could be activated separately in comparison to activating uncertainty in all channels simultaneously. Comparing outcomes of such computations reveal which channel of uncertainty is most consequential to the structuring of a prudent decision rule.[11]

---

[1]

This chapter draws heavily on a paper with the same title that was recently published in the Journal of Applied Econometrics by Hansen and Sargent entitled Risk, ambiguity and misspecification.

[2]

The term likelihood can have multiple meanings. We shall use it to represent a probability density of prize-relevant outcomes, which we refer to as repercussions, conditioned on parameters. Distinguishing likelihood functions from subjective priors is fundamental to Bayesian formulations of statistical learning. See [de Finetti, 1937], who recommended exchangeability as a more suitable assumption than iid (independent and identically distributed) to model situations in which a decision maker wants to learn. Putting subjective probabilities over parameters that index likelihood functions for iid sequences of random vectors generates exchangeable sequences of random variables.

[3]

We put “behavioral” in quotes to emphasize that most economic models are about agents’ behaviors, including models that impose the rational expectations and common knowledge assumptions that “behavioral” economists want to drop. “Behavioral” economics sometimes means work that is linked more or less informally to psychology.

[4]

Although we provide no formal links to psychology here, we think that a promising research plan would explore connections between so-called behavior distortions and the inferential challenges that economic decision makers confront. As is often assumed in behavioral models, degrees of confidence could differ across economic agents.

[5]

Statistical decision theory typically works with loss function which corresponds to negative of our the utility functions used here. This same observation carries over to their construction of risk functions.

[6]

Chamberlain uses a constraint on the family of prior distribution, consistent with the axiomatic formulation of [Gilboa and Schmeidler, 1989].

[7]

[Hansen and Miao, 2018] present a class of continuous-time diffusion models for which this distinction is particularly important. For an initial discussion of this distinction with links to other decision formulations, see [Hansen and Sargent, 2007].

[8]

While this contribution and some of the papers they cite, assume an endowment economy, their insights extend to a model with production.

[9]

Note that the endogenous state variable, \(K_{t}\), reveals no new information in addition to current and past values of the technology process. This means that there is no incentive for the investor to experiment in this setting.

[10]

By posing this as a date \(0\) commitment problem, we deliberately avoid dynamic consistency considerations.

[11]

[Cappelli et al., 2021] develop a related proposal with a similar ambition.